Preparando MOJI
A point belongs to a triangle if it lies inside the triangle or on one of its sides. Two triangles are disjoint if there is no point on the plane that belongs to both triangles.
You are given $$$n$$$ points on the plane. No two points coincide and no three points are collinear.
Find the number of different ways to choose two disjoint triangles with vertices in the given points. Two ways which differ only in order of triangles or in order of vertices inside triangles are considered equal.
The first line of the input contains an integer $$$n$$$ ($$$6 \le n \le 2000$$$) – the number of points.
Each of the next $$$n$$$ lines contains two integers $$$x_i$$$ and $$$y_i$$$ ($$$|x_i|, |y_i| \le 10^9$$$) – the coordinates of a point.
No two points coincide and no three points are collinear.
Print one integer – the number of ways to choose two disjoint triangles.
6
1 1
2 2
4 6
4 5
7 2
5 3
6
7
0 -1000000000
-5 -5
5 -5
-5 0
5 0
-2 2
2 2
21
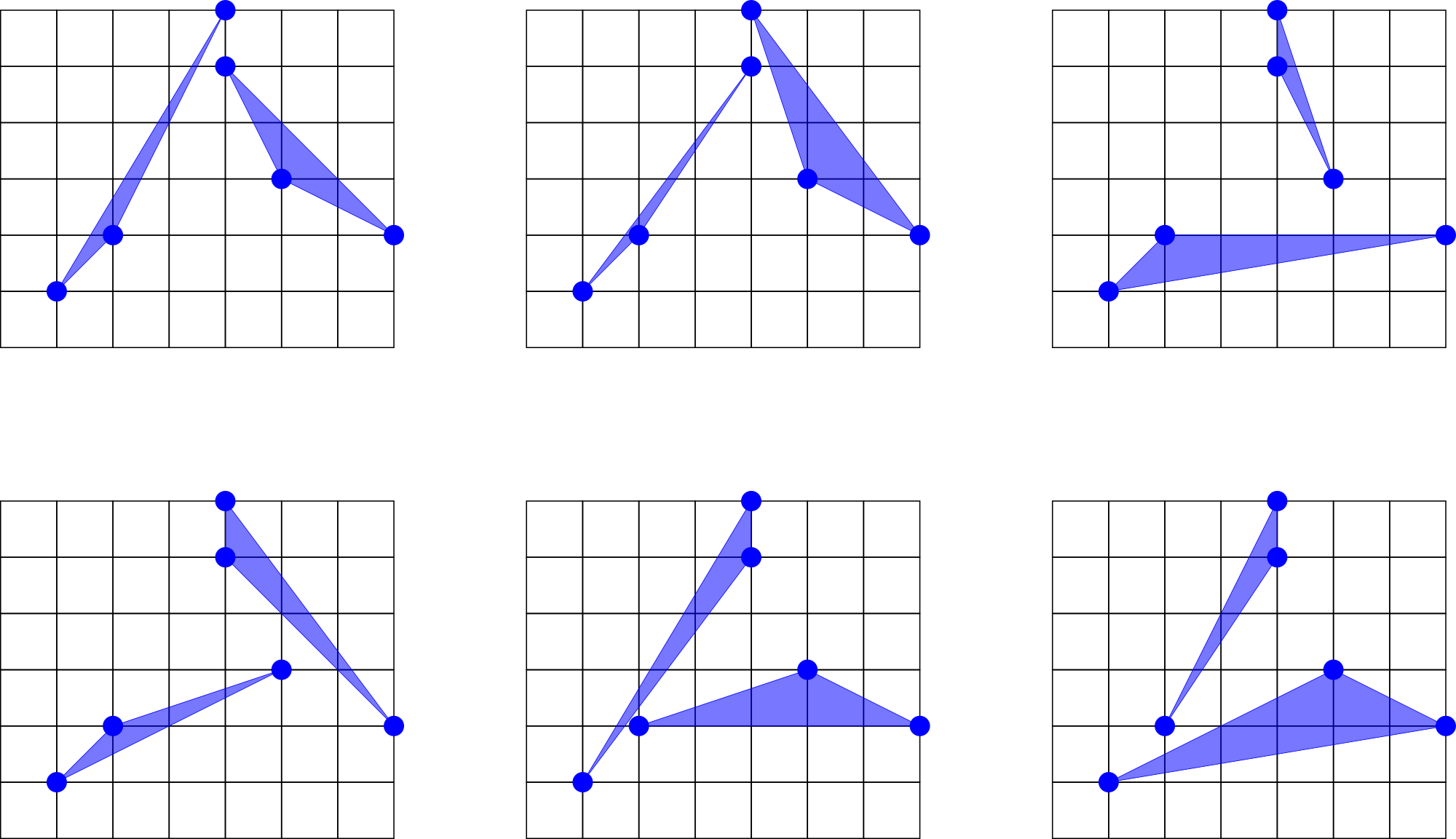
In the first example there are six pairs of disjoint triangles, they are shown on the picture below.
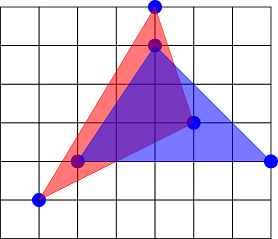
All other pairs of triangles are not disjoint, for example the following pair:
Informação
Provedor Codeforces
Código CF1025F
Tags
Submetido 0
BOUA! 0
Taxa de BOUA's 0%
Datas 09/05/2023 09:37:41
Relacionados