Covered Points

Description:

Input:

The first line contains a single integer $$$n$$$ ($$$1 \le n \le 1000$$$) — the number of segments.

Each of the next $$$n$$$ lines contains four integers $$$Ax_i, Ay_i, Bx_i, By_i$$$ ($$$-10^6 \le Ax_i, Ay_i, Bx_i, By_i \le 10^6$$$) — the coordinates of the endpoints $$$A$$$, $$$B$$$ ($$$A \ne B$$$) of the $$$i$$$-th segment.

It is guaranteed that no two segments lie on the same line.

Output:

Print a single integer — the number of distinct points with integer coordinates, which are covered by at least one segment.

Sample Input:

9
0 0 4 4
-1 5 4 0
4 0 4 4
5 2 11 2
6 1 6 7
5 6 11 6
10 1 10 7
7 0 9 8
10 -1 11 -1

Sample Output:

42

Sample Input:

4
-1 2 1 2
-1 0 1 0
-1 0 0 3
0 3 1 0

Sample Output:

7

Note:

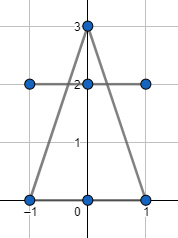
The image for the first example:

Several key points are marked blue, the answer contains some non-marked points as well.

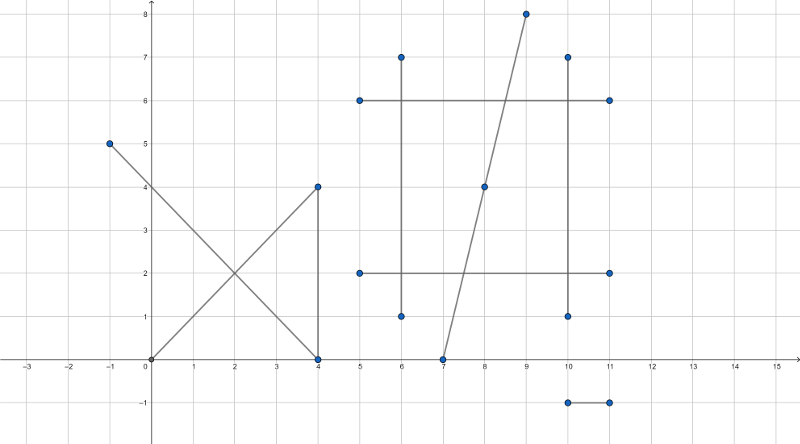
The image for the second example: