Ray in the tube

You are given a tube which is reflective inside represented as two non-coinciding, but parallel to $$$Ox$$$ lines. Each line has some special integer points — positions of sensors on sides of the tube.

You are going to emit a laser ray in the tube. To do so, you have to choose two integer points $$$A$$$ and $$$B$$$ on the first and the second line respectively (coordinates can be negative): the point $$$A$$$ is responsible for the position of the laser, and the point $$$B$$$ — for the direction of the laser ray. The laser ray is a ray starting at $$$A$$$ and directed at $$$B$$$ which will reflect from the sides of the tube (it doesn't matter if there are any sensors at a reflection point or not). A sensor will only register the ray if the ray hits exactly at the position of the sensor.

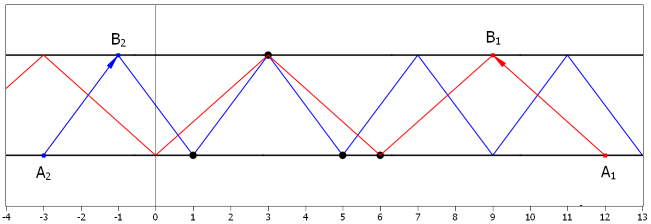Examples of laser rays. Note that image contains two examples. The $$$3$$$ sensors (denoted by black bold points on the tube sides) will register the blue ray but only $$$2$$$ will register the red.

Calculate the maximum number of sensors which can register your ray if you choose points $$$A$$$ and $$$B$$$ on the first and the second lines respectively.