Upgrading Cities

Description:

Input:

The first line of the input contains two integers $$$n$$$ and $$$m$$$ ($$$2 \le n \le 300\,000$$$, $$$1 \le m \le 300\,000$$$) — the number of cities and the number of one-way roads.

Next $$$m$$$ lines describe the road system of the kingdom. Each of them contains two integers $$$u_i$$$ and $$$v_i$$$ ($$$1 \le u_i, v_i \le n$$$, $$$u_i \neq v_i$$$), denoting one-way road from $$$u_i$$$ to $$$v_i$$$.

It is guaranteed, that the kingdoms' roads make an acyclic graph, which doesn't contain multiple edges and self-loops.

Output:

Print a single integer — the number of cities that the king has to upgrade.

Sample Input:

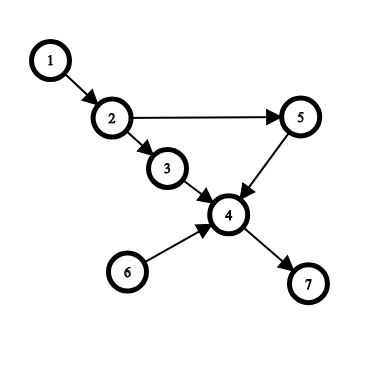
7 7
1 2
2 3
3 4
4 7
2 5
5 4
6 4

Sample Output:

4

Sample Input:

6 7
1 2
2 3
3 4
1 5
5 3
2 6
6 4

Sample Output:

4

Note:

In the first example:

• Starting at the city $$$1$$$ we can reach all the other cities, except for the city $$$6$$$. Also, from the city $$$6$$$ we cannot reach the city $$$1$$$. Therefore, if we destroy the city $$$6$$$ then the city $$$1$$$ will become important. So $$$1$$$ is a semi-important city.
• For city $$$2$$$, the set of cities that cannot reach $$$2$$$ and cannot be reached by $$$2$$$ is $$$\{6\}$$$. Therefore, destroying city $$$6$$$ will make the city $$$2$$$ important. So city $$$2$$$ is also semi-important.
• For city $$$3$$$, the set is $$$\{5, 6\}$$$. As you can see, destroying either city $$$5$$$ or $$$6$$$ will not make the city $$$3$$$ important. Therefore, it is neither important nor semi-important.
• For city $$$4$$$, the set is empty. So $$$4$$$ is an important city.
• The set for city $$$5$$$ is $$$\{3, 6\}$$$ and the set for city $$$6$$$ is $$$\{3, 5\}$$$. Similarly to city $$$3$$$, both of them are not important nor semi-important.
• The city $$$7$$$ is important since we can reach it from all other cities.

So we have two important cities ($$$4$$$ and $$$7$$$) and two semi-important cities ($$$1$$$ and $$$2$$$).

In the second example, the important cities are $$$1$$$ and $$$4$$$. The semi-important cities are $$$2$$$ and $$$3$$$.