Make It Equal

2000ms

262144K

Description:

There is a toy building consisting of $$$n$$$ towers. Each tower consists of several cubes standing on each other. The $$$i$$$-th tower consists of $$$h_i$$$ cubes, so it has height $$$h_i$$$.

Let's define operation slice on some height $$$H$$$ as following: for each tower $$$i$$$, if its height is greater than $$$H$$$, then remove some top cubes to make tower's height equal to $$$H$$$. Cost of one "slice" equals to the total number of removed cubes from all towers.

Let's name slice as good one if its cost is lower or equal to $$$k$$$ ($$$k \ge n$$$).

$\text{[math]}$

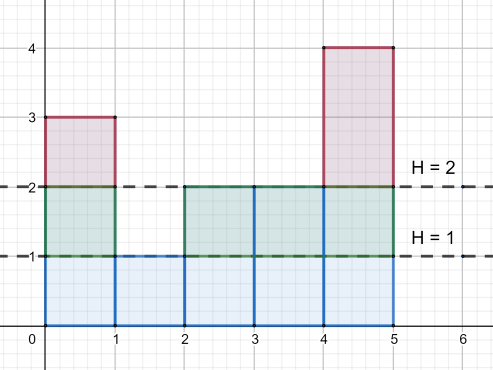
Calculate the minimum number of good slices you have to do to make all towers have the same height. Of course, it is always possible to make it so.

Input:

The first line contains two integers $$$n$$$ and $$$k$$$ ($$$1 \le n \le 2 \cdot 10^5$$$, $$$n \le k \le 10^9$$$) — the number of towers and the restriction on slices, respectively.

The second line contains $$$n$$$ space separated integers $$$h_1, h_2, \dots, h_n$$$ ($$$1 \le h_i \le 2 \cdot 10^5$$$) — the initial heights of towers.

Output:

Print one integer — the minimum number of good slices you have to do to make all towers have the same heigth.

Sample Input:

5 5
3 1 2 2 4

Sample Output:

Sample Input:

4 5
2 3 4 5

Sample Output:

Note:

In the first example it's optimal to make $$$2$$$ slices. The first slice is on height $$$2$$$ (its cost is $$$3$$$), and the second one is on height $$$1$$$ (its cost is $$$4$$$).

Informação

Provedor Codeforces

Código CF1065C