Tree with Maximum Cost

2000ms

262144K

Description:

You are given a tree consisting exactly of $$$n$$$ vertices. Tree is a connected undirected graph with $$$n-1$$$ edges. Each vertex $$$v$$$ of this tree has a value $$$a_v$$$ assigned to it.

Let $$$dist(x, y)$$$ be the distance between the vertices $$$x$$$ and $$$y$$$. The distance between the vertices is the number of edges on the simple path between them.

Let's define the cost of the tree as the following value: firstly, let's fix some vertex of the tree. Let it be $$$v$$$. Then the cost of the tree is $$$\sum\limits_{i = 1}^{n} dist(i, v) \cdot a_i$$$.

Your task is to calculate the maximum possible cost of the tree if you can choose $$$v$$$ arbitrarily.

Input:

The first line contains one integer $$$n$$$, the number of vertices in the tree ($$$1 \le n \le 2 \cdot 10^5$$$).

The second line of the input contains $$$n$$$ integers $$$a_1, a_2, \dots, a_n$$$ ($$$1 \le a_i \le 2 \cdot 10^5$$$), where $$$a_i$$$ is the value of the vertex $$$i$$$.

Each of the next $$$n - 1$$$ lines describes an edge of the tree. Edge $$$i$$$ is denoted by two integers $$$u_i$$$ and $$$v_i$$$, the labels of vertices it connects ($$$1 \le u_i, v_i \le n$$$, $$$u_i \ne v_i$$$).

It is guaranteed that the given edges form a tree.

Output:

Print one integer — the maximum possible cost of the tree if you can choose any vertex as $$$v$$$.

Sample Input:

8
9 4 1 7 10 1 6 5
1 2
2 3
1 4
1 5
5 6
5 7
5 8

Sample Output:

Sample Input:

1
1337

Sample Output:

Note:

Picture corresponding to the first example: 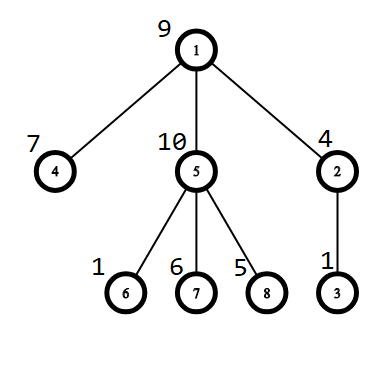$\text{[math]}$

You can choose the vertex $$$3$$$ as a root, then the answer will be $$$2 \cdot 9 + 1 \cdot 4 + 0 \cdot 1 + 3 \cdot 7 + 3 \cdot 10 + 4 \cdot 1 + 4 \cdot 6 + 4 \cdot 5 = 18 + 4 + 0 + 21 + 30 + 4 + 24 + 20 = 121$$$.

In the second example tree consists only of one vertex so the answer is always $$$0$$$.

Informação

Provedor Codeforces

Código CF1092F