Preparando MOJI
You are given an angle $$$\text{ang}$$$.
The Jury asks You to find such regular $$$n$$$-gon (regular polygon with $$$n$$$ vertices) that it has three vertices $$$a$$$, $$$b$$$ and $$$c$$$ (they can be non-consecutive) with $$$\angle{abc} = \text{ang}$$$ or report that there is no such $$$n$$$-gon.
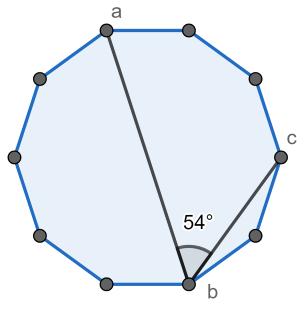
If there are several answers, print the minimal one. It is guarantied that if answer exists then it doesn't exceed $$$998244353$$$.
The first line contains single integer $$$T$$$ ($$$1 \le T \le 180$$$) — the number of queries.
Each of the next $$$T$$$ lines contains one integer $$$\text{ang}$$$ ($$$1 \le \text{ang} < 180$$$) — the angle measured in degrees.
For each query print single integer $$$n$$$ ($$$3 \le n \le 998244353$$$) — minimal possible number of vertices in the regular $$$n$$$-gon or $$$-1$$$ if there is no such $$$n$$$.
4 54 50 2 178
10 18 90 180
The answer for the first query is on the picture above.
The answer for the second query is reached on a regular $$$18$$$-gon. For example, $$$\angle{v_2 v_1 v_6} = 50^{\circ}$$$.
The example angle for the third query is $$$\angle{v_{11} v_{10} v_{12}} = 2^{\circ}$$$.
In the fourth query, minimal possible $$$n$$$ is $$$180$$$ (not $$$90$$$).