Edgy Trees

2000ms

262144K

Description:

You are given a tree (a connected undirected graph without cycles) of $$$n$$$ vertices. Each of the $$$n - 1$$$ edges of the tree is colored in either black or red.

You are also given an integer $$$k$$$. Consider sequences of $$$k$$$ vertices. Let's call a sequence $$$[a_1, a_2, \ldots, a_k]$$$ good if it satisfies the following criterion:

We will walk a path (possibly visiting same edge/vertex multiple times) on the tree, starting from $$$a_1$$$ and ending at $$$a_k$$$.
Start at $$$a_1$$$, then go to $$$a_2$$$ using the shortest path between $$$a_1$$$ and $$$a_2$$$, then go to $$$a_3$$$ in a similar way, and so on, until you travel the shortest path between $$$a_{k-1}$$$ and $$$a_k$$$.
If you walked over at least one black edge during this process, then the sequence is good.

$\text{[math]}$

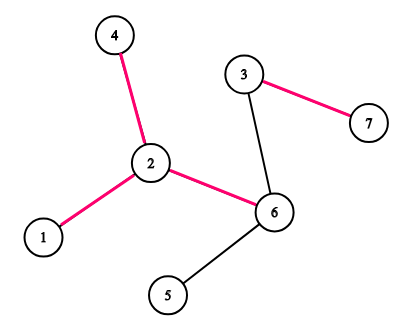
Consider the tree on the picture. If $$$k=3$$$ then the following sequences are good: $$$[1, 4, 7]$$$, $$$[5, 5, 3]$$$ and $$$[2, 3, 7]$$$. The following sequences are not good: $$$[1, 4, 6]$$$, $$$[5, 5, 5]$$$, $$$[3, 7, 3]$$$.

There are $$$n^k$$$ sequences of vertices, count how many of them are good. Since this number can be quite large, print it modulo $$$10^9+7$$$.

Input:

The first line contains two integers $$$n$$$ and $$$k$$$ ($$$2 \le n \le 10^5$$$, $$$2 \le k \le 100$$$), the size of the tree and the length of the vertex sequence.

Each of the next $$$n - 1$$$ lines contains three integers $$$u_i$$$, $$$v_i$$$ and $$$x_i$$$ ($$$1 \le u_i, v_i \le n$$$, $$$x_i \in \{0, 1\}$$$), where $$$u_i$$$ and $$$v_i$$$ denote the endpoints of the corresponding edge and $$$x_i$$$ is the color of this edge ($$$0$$$ denotes red edge and $$$1$$$ denotes black edge).

Output:

Print the number of good sequences modulo $$$10^9 + 7$$$.

Sample Input:

Sample Output:

Sample Input:

Sample Output:

Sample Input:

3 5
1 2 1
2 3 0

Sample Output:

Note:

In the first example, all sequences ($$$4^4$$$) of length $$$4$$$ except the following are good:

$$$[1, 1, 1, 1]$$$
$$$[2, 2, 2, 2]$$$
$$$[3, 3, 3, 3]$$$
$$$[4, 4, 4, 4]$$$

In the second example, all edges are red, hence there aren't any good sequences.

Informação

Provedor Codeforces

Código CF1139C