Queen

1000ms

262144K

Description:

You are given a rooted tree with vertices numerated from $$$1$$$ to $$$n$$$. A tree is a connected graph without cycles. A rooted tree has a special vertex named root.

Ancestors of the vertex $$$i$$$ are all vertices on the path from the root to the vertex $$$i$$$, except the vertex $$$i$$$ itself. The parent of the vertex $$$i$$$ is the nearest to the vertex $$$i$$$ ancestor of $$$i$$$. Each vertex is a child of its parent. In the given tree the parent of the vertex $$$i$$$ is the vertex $$$p_i$$$. For the root, the value $$$p_i$$$ is $$$-1$$$.

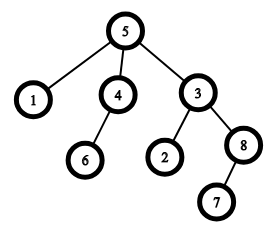$\text{[math]}$ An example of a tree with $$$n=8$$$, the root is vertex $$$5$$$. The parent of the vertex $$$2$$$ is vertex $$$3$$$, the parent of the vertex $$$1$$$ is vertex $$$5$$$. The ancestors of the vertex $$$6$$$ are vertices $$$4$$$ and $$$5$$$, the ancestors of the vertex $$$7$$$ are vertices $$$8$$$, $$$3$$$ and $$$5$$$

You noticed that some vertices do not respect others. In particular, if $$$c_i = 1$$$, then the vertex $$$i$$$ does not respect any of its ancestors, and if $$$c_i = 0$$$, it respects all of them.

You decided to delete vertices from the tree one by one. On each step you select such a non-root vertex that it does not respect its parent and none of its children respects it. If there are several such vertices, you select the one with the smallest number. When you delete this vertex $$$v$$$, all children of $$$v$$$ become connected with the parent of $$$v$$$.

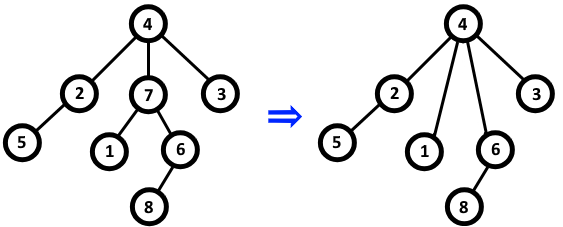$\text{[math]}$ An example of deletion of the vertex $$$7$$$.

Once there are no vertices matching the criteria for deletion, you stop the process. Print the order in which you will delete the vertices. Note that this order is unique.

Input:

The first line contains a single integer $$$n$$$ ($$$1 \le n \le 10^5$$$) — the number of vertices in the tree.

The next $$$n$$$ lines describe the tree: the $$$i$$$-th line contains two integers $$$p_i$$$ and $$$c_i$$$ ($$$1 \le p_i \le n$$$, $$$0 \le c_i \le 1$$$), where $$$p_i$$$ is the parent of the vertex $$$i$$$, and $$$c_i = 0$$$, if the vertex $$$i$$$ respects its parents, and $$$c_i = 1$$$, if the vertex $$$i$$$ does not respect any of its parents. The root of the tree has $$$-1$$$ instead of the parent index, also, $$$c_i=0$$$ for the root. It is guaranteed that the values $$$p_i$$$ define a rooted tree with $$$n$$$ vertices.

Output:

In case there is at least one vertex to delete, print the only line containing the indices of the vertices you will delete in the order you delete them. Otherwise print a single integer $$$-1$$$.

Sample Input:

Sample Output:

1 2 4

Sample Input:

Sample Output:

-1

Sample Input:

Sample Output:

Note:

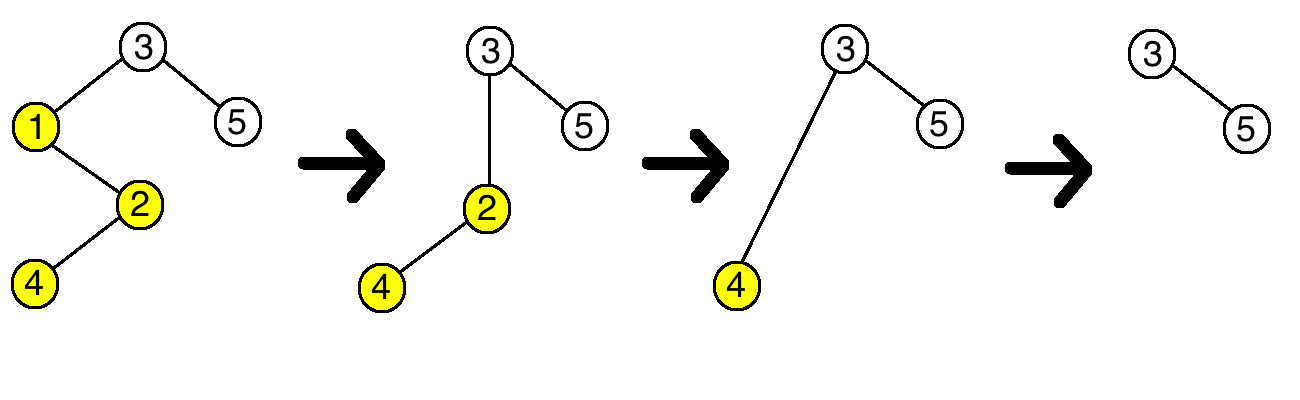
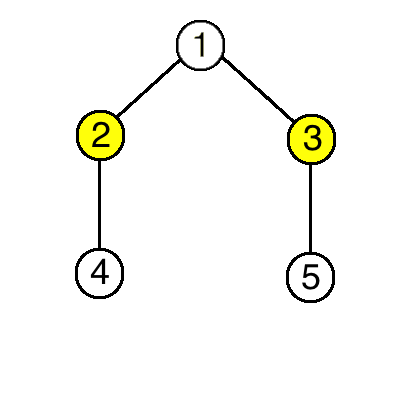
The deletion process in the first example is as follows (see the picture below, the vertices with $$$c_i=1$$$ are in yellow):

first you will delete the vertex $$$1$$$, because it does not respect ancestors and all its children (the vertex $$$2$$$) do not respect it, and $$$1$$$ is the smallest index among such vertices;
the vertex $$$2$$$ will be connected with the vertex $$$3$$$ after deletion;
then you will delete the vertex $$$2$$$, because it does not respect ancestors and all its children (the only vertex $$$4$$$) do not respect it;
the vertex $$$4$$$ will be connected with the vertex $$$3$$$;
then you will delete the vertex $$$4$$$, because it does not respect ancestors and all its children (there are none) do not respect it (vacuous truth);
you will just delete the vertex $$$4$$$;
there are no more vertices to delete.

$\text{[math]}$

In the second example you don't need to delete any vertex:

vertices $$$2$$$ and $$$3$$$ have children that respect them;
vertices $$$4$$$ and $$$5$$$ respect ancestors.

$\text{[math]}$

In the third example the tree will change this way:

$\text{[math]}$

Informação

Provedor Codeforces

Código CF1143C