Leaf Partition

1000ms

262144K

Description:

You are given a rooted tree with $$$n$$$ nodes, labeled from $$$1$$$ to $$$n$$$. The tree is rooted at node $$$1$$$. The parent of the $$$i$$$-th node is $$$p_i$$$. A leaf is node with no children. For a given set of leaves $$$L$$$, let $$$f(L)$$$ denote the smallest connected subgraph that contains all leaves $$$L$$$.

You would like to partition the leaves such that for any two different sets $$$x, y$$$ of the partition, $$$f(x)$$$ and $$$f(y)$$$ are disjoint.

Count the number of ways to partition the leaves, modulo $$$998244353$$$. Two ways are different if there are two leaves such that they are in the same set in one way but in different sets in the other.

Input:

The first line contains an integer $$$n$$$ ($$$2 \leq n \leq 200\,000$$$) — the number of nodes in the tree.

The next line contains $$$n-1$$$ integers $$$p_2, p_3, \ldots, p_n$$$ ($$$1 \leq p_i < i$$$).

Output:

Print a single integer, the number of ways to partition the leaves, modulo $$$998244353$$$.

Sample Input:

5
1 1 1 1

Sample Output:

Sample Input:

10
1 2 3 4 5 6 7 8 9

Sample Output:

Note:

In the first example, the leaf nodes are $$$2,3,4,5$$$. The ways to partition the leaves are in the following image 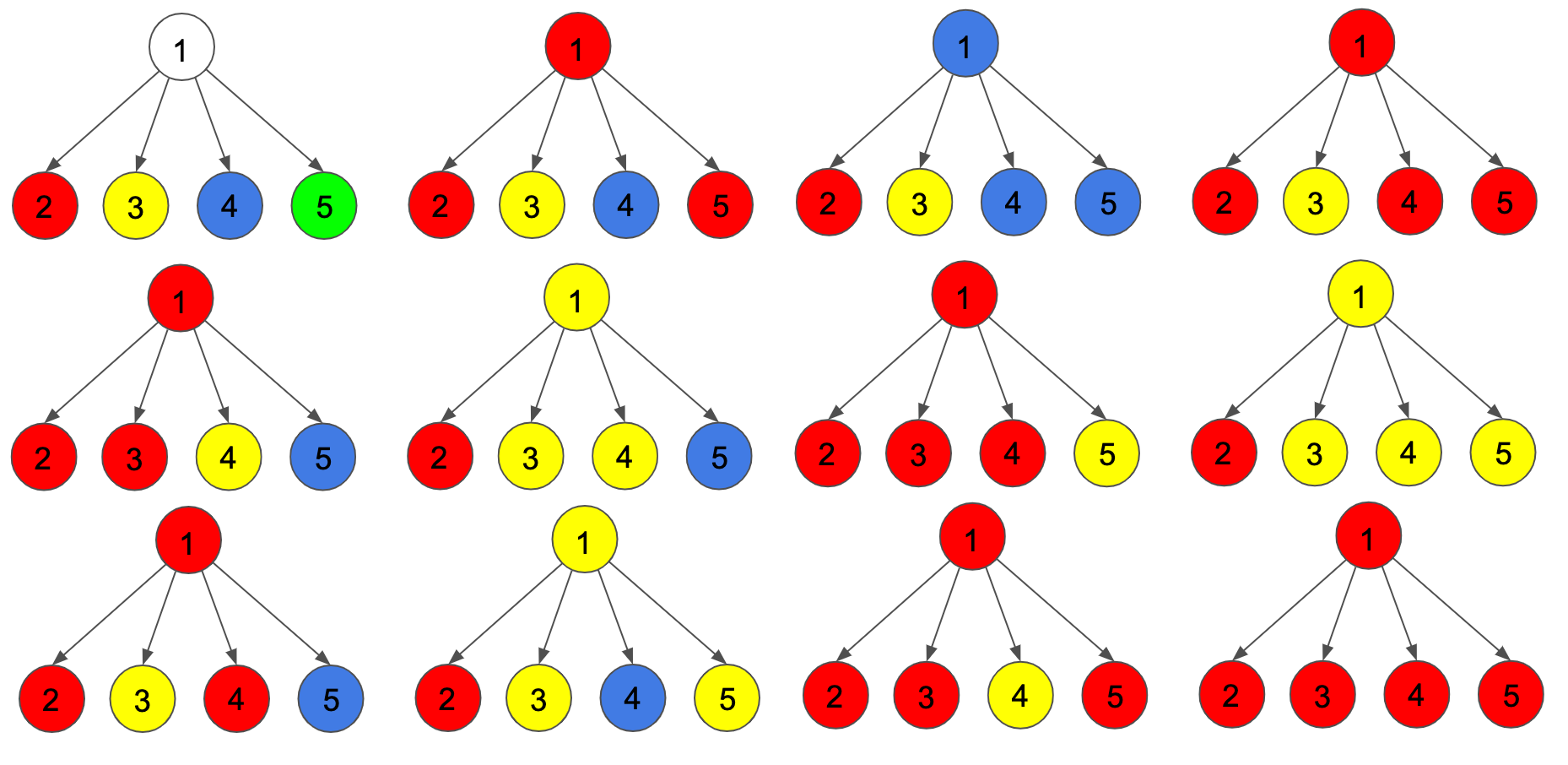$\text{[math]}$

In the second example, the only leaf is node $$$10$$$ so there is only one partition. Note that node $$$1$$$ is not a leaf.

Informação

Provedor Codeforces

Código CF1146F