Satanic Panic

4000ms

262144K

Description:

You are given a set of $$$n$$$ points in a 2D plane. No three points are collinear.

A pentagram is a set of $$$5$$$ points $$$A,B,C,D,E$$$ that can be arranged as follows. 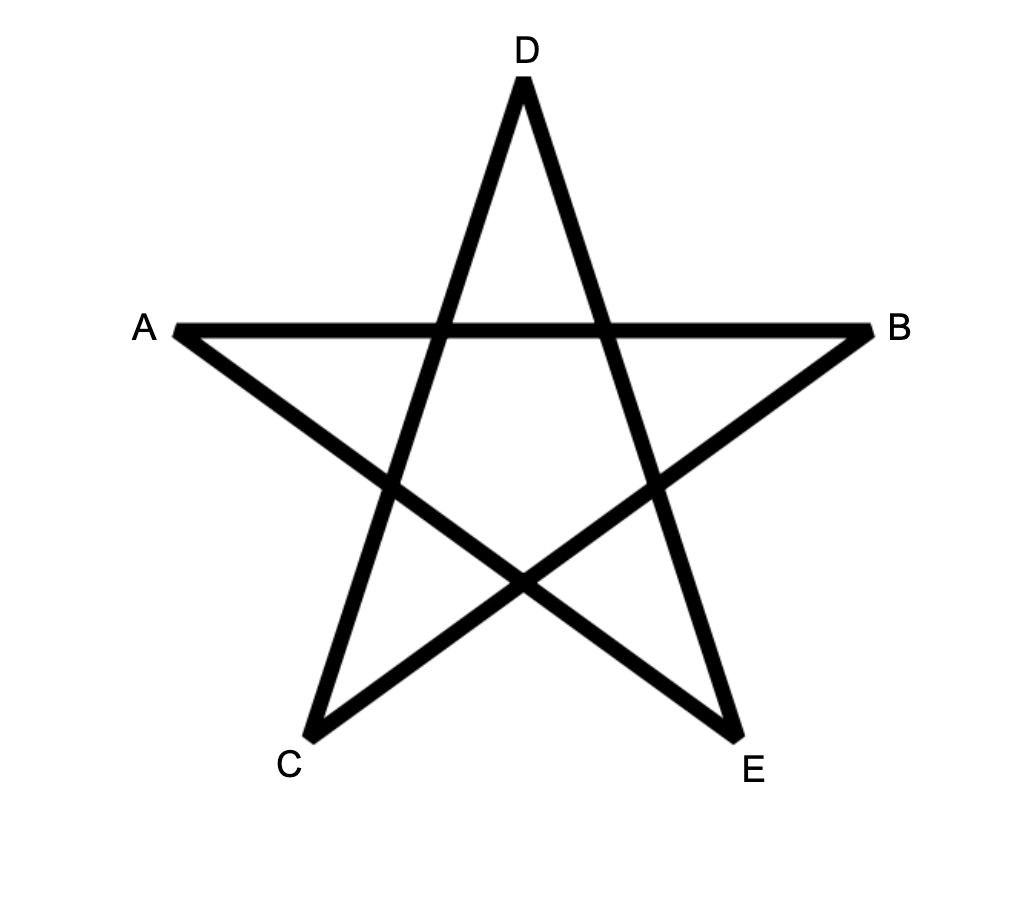$\text{[math]}$ Note the length of the line segments don't matter, only that those particular intersections exist.

Count the number of ways to choose $$$5$$$ points from the given set that form a pentagram.

Input:

The first line contains an integer $$$n$$$ ($$$5 \leq n \leq 300$$$) — the number of points.

Each of the next $$$n$$$ lines contains two integers $$$x_i, y_i$$$ ($$$-10^6 \leq x_i,y_i \leq 10^6$$$) — the coordinates of the $$$i$$$-th point. It is guaranteed that no three points are collinear.

Output:

Print a single integer, the number of sets of $$$5$$$ points that form a pentagram.

Sample Input:

Sample Output:

Sample Input:

Sample Output:

Sample Input:

10
841746 527518
595261 331297
-946901 129987
670374 -140388
-684770 309555
-302589 415564
-387435 613331
-624940 -95922
945847 -199224
24636 -565799

Sample Output:

Note:

A picture of the first sample: $\text{[math]}$ A picture of the second sample: $\text{[math]}$ A picture of the third sample: $\text{[math]}$

Informação

Provedor Codeforces

Código CF1146H