Preparando MOJI
This is an interactive problem.
You're given a tree consisting of $$$n$$$ nodes, rooted at node $$$1$$$. A tree is a connected graph with no cycles.
We chose a hidden node $$$x$$$. In order to find this node, you can ask queries of two types:
Node $$$a$$$ is called an ancestor of node $$$b$$$ if $$$a \ne b$$$ and the shortest path from node $$$1$$$ to node $$$b$$$ passes through node $$$a$$$. Note that in this problem a node is not an ancestor of itself.
Can you find $$$x$$$ in no more than $$$36$$$ queries? The hidden node is fixed in each test beforehand and does not depend on your queries.
To ask a question, print it in one of the formats above:
After each question, you should read the answer: either the distance or the second vertex on the path, as mentioned in the legend.
If we answer with $$$-1$$$ instead of a valid answer, that means you exceeded the number of queries, made an invalid query, or violated the condition in the second type of queries. Exit immediately after receiving $$$-1$$$ and you will see Wrong answer verdict. Otherwise, you can get an arbitrary verdict because your solution will continue to read from a closed stream.
After printing a query, do not forget to output end of line and flush the output. Otherwise, you will get Idleness limit exceeded. To do this, use:
Hacks:
The first line should contain two integers $$$n$$$ and $$$x$$$ ($$$2 \le n \le 2 \cdot 10^5$$$, $$$1 \le x \le n$$$).
Each of the next $$$n-1$$$ lines should contain two integers $$$u$$$ and $$$v$$$ ($$$1 \le u,v \le n$$$) that mean there is an edge between nodes $$$u$$$ and $$$v$$$. The edges must form a tree.
The first line contains the integer $$$n$$$ ($$$2 \le n \le 2 \cdot 10^5$$$) — the number of nodes in the tree.
Each of the next $$$n-1$$$ lines contains two space-separated integers $$$u$$$ and $$$v$$$ ($$$1 \le u,v \le n$$$) that mean there's an edge between nodes $$$u$$$ and $$$v$$$. It's guaranteed that the given graph is a tree.
To print the answer, print "! x" (without quotes).
5 1 2 1 3 3 4 3 5 3 5
d 2 s 3 ! 5
In the first example, the hidden node is node $$$5$$$.
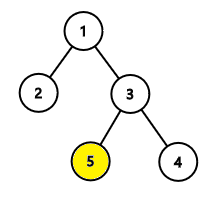
We first ask about the distance between node $$$x$$$ and node $$$2$$$. The answer is $$$3$$$, so node $$$x$$$ is either $$$4$$$ or $$$5$$$. We then ask about the second node in the path from node $$$3$$$ to node $$$x$$$. Note here that node $$$3$$$ is an ancestor of node $$$5$$$. We receive node $$$5$$$ as the answer. Finally, we report that the hidden node is node $$$5$$$.