Preparando MOJI
This is the first subtask of problem F. The only differences between this and the second subtask are the constraints on the value of $$$m$$$ and the time limit. You need to solve both subtasks in order to hack this one.
There are $$$n+1$$$ distinct colours in the universe, numbered $$$0$$$ through $$$n$$$. There is a strip of paper $$$m$$$ centimetres long initially painted with colour $$$0$$$.
Alice took a brush and painted the strip using the following process. For each $$$i$$$ from $$$1$$$ to $$$n$$$, in this order, she picks two integers $$$0 \leq a_i < b_i \leq m$$$, such that the segment $$$[a_i, b_i]$$$ is currently painted with a single colour, and repaints it with colour $$$i$$$.
Alice chose the segments in such a way that each centimetre is now painted in some colour other than $$$0$$$. Formally, the segment $$$[i-1, i]$$$ is painted with colour $$$c_i$$$ ($$$c_i \neq 0$$$). Every colour other than $$$0$$$ is visible on the strip.
Count the number of different pairs of sequences $$$\{a_i\}_{i=1}^n$$$, $$$\{b_i\}_{i=1}^n$$$ that result in this configuration.
Since this number may be large, output it modulo $$$998244353$$$.
The first line contains a two integers $$$n$$$, $$$m$$$ ($$$1 \leq n \leq 500$$$, $$$n = m$$$) — the number of colours excluding the colour $$$0$$$ and the length of the paper, respectively.
The second line contains $$$m$$$ space separated integers $$$c_1, c_2, \ldots, c_m$$$ ($$$1 \leq c_i \leq n$$$) — the colour visible on the segment $$$[i-1, i]$$$ after the process ends. It is guaranteed that for all $$$j$$$ between $$$1$$$ and $$$n$$$ there is an index $$$k$$$ such that $$$c_k = j$$$.
Note that since in this subtask $$$n = m$$$, this means that $$$c$$$ is a permutation of integers $$$1$$$ through $$$n$$$.
Output a single integer — the number of ways Alice can perform the painting, modulo $$$998244353$$$.
3 3 1 2 3
5
7 7 4 5 1 6 2 3 7
165
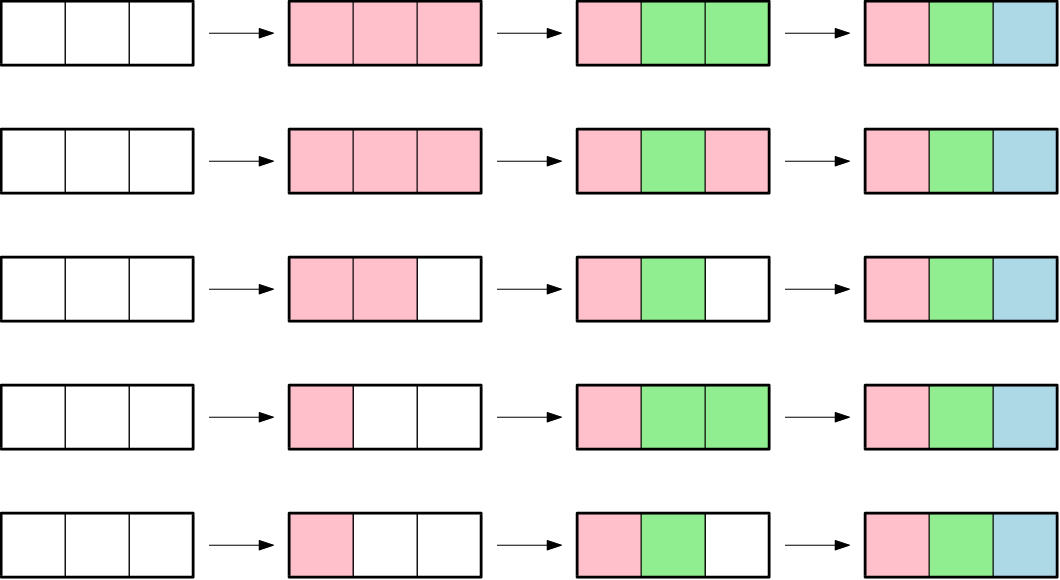
In the first example, there are $$$5$$$ ways, all depicted in the figure below. Here, $$$0$$$ is white, $$$1$$$ is red, $$$2$$$ is green and $$$3$$$ is blue.
Below is an example of a painting process that is not valid, as in the second step the segment 1 3 is not single colour, and thus may not be repainted with colour $$$2$$$.
Informação
Provedor Codeforces
Código CF1178F1
Tags
Submetido 0
BOUA! 0
Taxa de BOUA's 0%
Datas 09/05/2023 09:48:45
Relacionados