Alex and a Rhombus

1000ms

262144K

Description:

While playing with geometric figures Alex has accidentally invented a concept of a $$$n$$$-th order rhombus in a cell grid.

A $$$1$$$-st order rhombus is just a square $$$1 \times 1$$$ (i.e just a cell).

A $$$n$$$-th order rhombus for all $$$n \geq 2$$$ one obtains from a $$$n-1$$$-th order rhombus adding all cells which have a common side with it to it (look at the picture to understand it better).

$\text{[math]}$

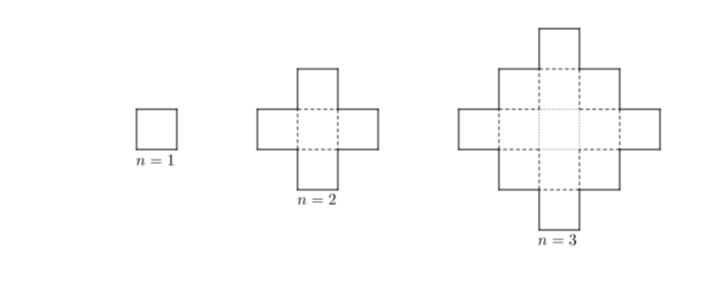
Alex asks you to compute the number of cells in a $$$n$$$-th order rhombus.

Input:

The first and only input line contains integer $$$n$$$ ($$$1 \leq n \leq 100$$$) — order of a rhombus whose numbers of cells should be computed.

Output:

Print exactly one integer — the number of cells in a $$$n$$$-th order rhombus.

Sample Input:

Sample Output:

Sample Input:

Sample Output:

Sample Input:

Sample Output:

Note:

Images of rhombus corresponding to the examples are given in the statement.

Informação

Provedor Codeforces

Código CF1180A