Tokitsukaze and Strange Rectangle

3000ms

262144K

Description:

There are $$$n$$$ points on the plane, the $$$i$$$-th of which is at $$$(x_i, y_i)$$$. Tokitsukaze wants to draw a strange rectangular area and pick all the points in the area.

The strange area is enclosed by three lines, $$$x = l$$$, $$$y = a$$$ and $$$x = r$$$, as its left side, its bottom side and its right side respectively, where $$$l$$$, $$$r$$$ and $$$a$$$ can be any real numbers satisfying that $$$l < r$$$. The upper side of the area is boundless, which you can regard as a line parallel to the $$$x$$$-axis at infinity. The following figure shows a strange rectangular area.

$\text{[math]}$

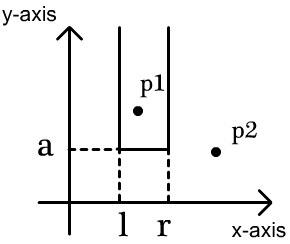
A point $$$(x_i, y_i)$$$ is in the strange rectangular area if and only if $$$l < x_i < r$$$ and $$$y_i > a$$$. For example, in the above figure, $$$p_1$$$ is in the area while $$$p_2$$$ is not.

Tokitsukaze wants to know how many different non-empty sets she can obtain by picking all the points in a strange rectangular area, where we think two sets are different if there exists at least one point in one set of them but not in the other.

Input:

The first line contains a single integer $$$n$$$ ($$$1 \leq n \leq 2 \times 10^5$$$) — the number of points on the plane.

The $$$i$$$-th of the next $$$n$$$ lines contains two integers $$$x_i$$$, $$$y_i$$$ ($$$1 \leq x_i, y_i \leq 10^9$$$) — the coordinates of the $$$i$$$-th point.

All points are distinct.

Output:

Print a single integer — the number of different non-empty sets of points she can obtain.

Sample Input:

Sample Output:

Sample Input:

Sample Output:

Sample Input:

Sample Output:

Note:

For the first example, there is exactly one set having $$$k$$$ points for $$$k = 1, 2, 3$$$, so the total number is $$$3$$$.

For the second example, the numbers of sets having $$$k$$$ points for $$$k = 1, 2, 3$$$ are $$$3$$$, $$$2$$$, $$$1$$$ respectively, and their sum is $$$6$$$.

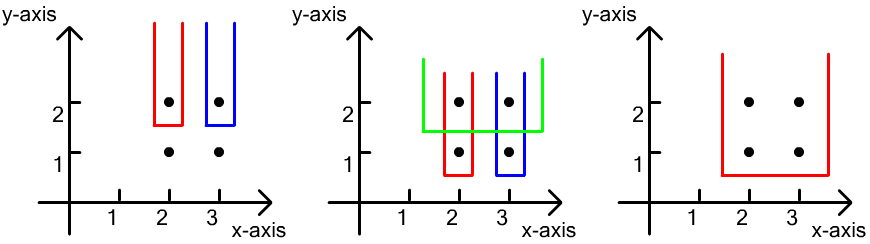
For the third example, as the following figure shows, there are

$$$2$$$ sets having one point;
$$$3$$$ sets having two points;
$$$1$$$ set having four points.

Therefore, the number of different non-empty sets in this example is $$$2 + 3 + 0 + 1 = 6$$$.

$\text{[math]}$

Informação

Provedor Codeforces

Código CF1190D