Rectangle Painting 1

1000ms

262144K

Description:

There is a square grid of size $$$n \times n$$$. Some cells are colored in black, all others are colored in white. In one operation you can select some rectangle and color all its cells in white. It costs $$$\max(h, w)$$$ to color a rectangle of size $$$h \times w$$$. You are to make all cells white for minimum total cost.

Input:

The first line contains a single integer $$$n$$$ ($$$1 \leq n \leq 50$$$) — the size of the square grid.

Each of the next $$$n$$$ lines contains a string of length $$$n$$$, consisting of characters '.' and '#'. The $$$j$$$-th character of the $$$i$$$-th line is '#' if the cell with coordinates $$$(i, j)$$$ is black, otherwise it is white.

Output:

Print a single integer — the minimum total cost to paint all cells in white.

Sample Input:

3
###
#.#
###

Sample Output:

Sample Input:

3
...
...
...

Sample Output:

Sample Input:

4
#...
....
....
#...

Sample Output:

Sample Input:

5
#...#
.#.#.
.....
.#...
#....

Sample Output:

Note:

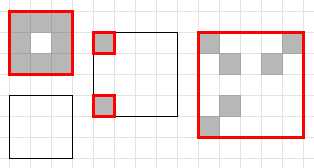
The examples and some of optimal solutions are shown on the pictures below.

$\text{[math]}$

Informação

Provedor Codeforces

Código CF1198D