Water Lily

1000ms

262144K

Description:

While sailing on a boat, Inessa noticed a beautiful water lily flower above the lake's surface. She came closer and it turned out that the lily was exactly $$$H$$$ centimeters above the water surface. Inessa grabbed the flower and sailed the distance of $$$L$$$ centimeters. Exactly at this point the flower touched the water surface.

$\text{[math]}$

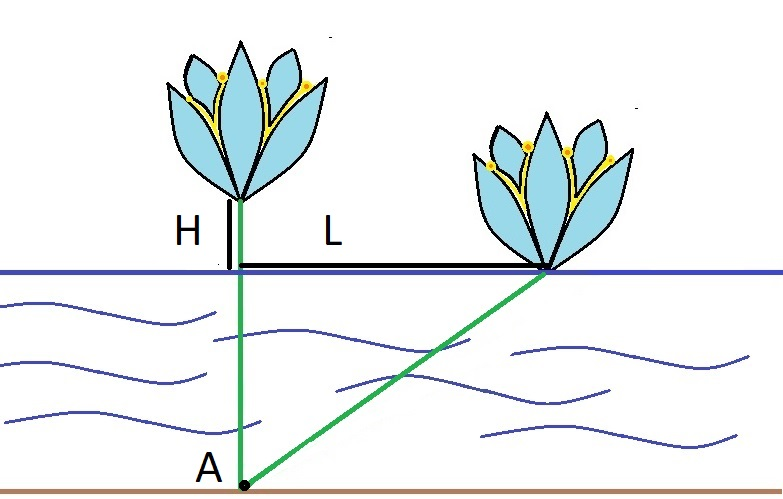
Suppose that the lily grows at some point $$$A$$$ on the lake bottom, and its stem is always a straight segment with one endpoint at point $$$A$$$. Also suppose that initially the flower was exactly above the point $$$A$$$, i.e. its stem was vertical. Can you determine the depth of the lake at point $$$A$$$?

Input:

The only line contains two integers $$$H$$$ and $$$L$$$ ($$$1 \le H < L \le 10^{6}$$$).

Output:

Print a single number — the depth of the lake at point $$$A$$$. The absolute or relative error should not exceed $$$10^{-6}$$$.

Formally, let your answer be $$$A$$$, and the jury's answer be $$$B$$$. Your answer is accepted if and only if $$$\frac{|A - B|}{\max{(1, |B|)}} \le 10^{-6}$$$.

Sample Input:

1 2

Sample Output:

1.5000000000000

Sample Input:

3 5

Sample Output:

2.6666666666667

Informação

Provedor Codeforces

Código CF1199B