Graph Traveler

2000ms

524288K

Description:

Gildong is experimenting with an interesting machine Graph Traveler. In Graph Traveler, there is a directed graph consisting of $$$n$$$ vertices numbered from $$$1$$$ to $$$n$$$. The $$$i$$$-th vertex has $$$m_i$$$ outgoing edges that are labeled as $$$e_i[0]$$$, $$$e_i[1]$$$, $$$\ldots$$$, $$$e_i[m_i-1]$$$, each representing the destination vertex of the edge. The graph can have multiple edges and self-loops. The $$$i$$$-th vertex also has an integer $$$k_i$$$ written on itself.

A travel on this graph works as follows.

Gildong chooses a vertex to start from, and an integer to start with. Set the variable $$$c$$$ to this integer.
After arriving at the vertex $$$i$$$, or when Gildong begins the travel at some vertex $$$i$$$, add $$$k_i$$$ to $$$c$$$.
The next vertex is $$$e_i[x]$$$ where $$$x$$$ is an integer $$$0 \le x \le m_i-1$$$ satisfying $$$x \equiv c \pmod {m_i}$$$. Go to the next vertex and go back to step 2.

It's obvious that a travel never ends, since the 2nd and the 3rd step will be repeated endlessly.

For example, assume that Gildong starts at vertex $$$1$$$ with $$$c = 5$$$, and $$$m_1 = 2$$$, $$$e_1[0] = 1$$$, $$$e_1[1] = 2$$$, $$$k_1 = -3$$$. Right after he starts at vertex $$$1$$$, $$$c$$$ becomes $$$2$$$. Since the only integer $$$x$$$ ($$$0 \le x \le 1$$$) where $$$x \equiv c \pmod {m_i}$$$ is $$$0$$$, Gildong goes to vertex $$$e_1[0] = 1$$$. After arriving at vertex $$$1$$$ again, $$$c$$$ becomes $$$-1$$$. The only integer $$$x$$$ satisfying the conditions is $$$1$$$, so he goes to vertex $$$e_1[1] = 2$$$, and so on.

Since Gildong is quite inquisitive, he's going to ask you $$$q$$$ queries. He wants to know how many distinct vertices will be visited infinitely many times, if he starts the travel from a certain vertex with a certain value of $$$c$$$. Note that you should not count the vertices that will be visited only finite times.

Input:

The first line of the input contains an integer $$$n$$$ ($$$1 \le n \le 1000$$$), the number of vertices in the graph.

The second line contains $$$n$$$ integers. The $$$i$$$-th integer is $$$k_i$$$ ($$$-10^9 \le k_i \le 10^9$$$), the integer written on the $$$i$$$-th vertex.

Next $$$2 \cdot n$$$ lines describe the edges of each vertex. The $$$(2 \cdot i + 1)$$$-st line contains an integer $$$m_i$$$ ($$$1 \le m_i \le 10$$$), the number of outgoing edges of the $$$i$$$-th vertex. The $$$(2 \cdot i + 2)$$$-nd line contains $$$m_i$$$ integers $$$e_i[0]$$$, $$$e_i[1]$$$, $$$\ldots$$$, $$$e_i[m_i-1]$$$, each having an integer value between $$$1$$$ and $$$n$$$, inclusive.

Next line contains an integer $$$q$$$ ($$$1 \le q \le 10^5$$$), the number of queries Gildong wants to ask.

Next $$$q$$$ lines contains two integers $$$x$$$ and $$$y$$$ ($$$1 \le x \le n$$$, $$$-10^9 \le y \le 10^9$$$) each, which mean that the start vertex is $$$x$$$ and the starting value of $$$c$$$ is $$$y$$$.

Output:

For each query, print the number of distinct vertices that will be visited infinitely many times, if Gildong starts at vertex $$$x$$$ with starting integer $$$y$$$.

Sample Input:

Sample Output:

Sample Input:

Sample Output:

Note:

The first example can be shown like the following image:

$\text{[math]}$

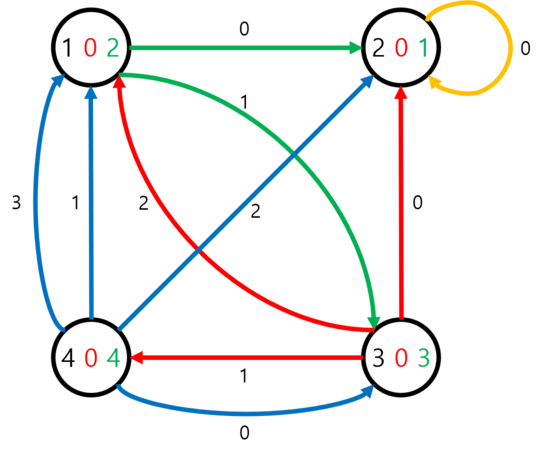
Three integers are marked on $$$i$$$-th vertex: $$$i$$$, $$$k_i$$$, and $$$m_i$$$ respectively. The outgoing edges are labeled with an integer representing the edge number of $$$i$$$-th vertex.

The travel for each query works as follows. It is described as a sequence of phrases, each in the format "vertex ($$$c$$$ after $$$k_i$$$ added)".

$$$1(0) \to 2(0) \to 2(0) \to \ldots$$$
$$$2(0) \to 2(0) \to \ldots$$$
$$$3(-1) \to 1(-1) \to 3(-1) \to \ldots$$$
$$$4(-2) \to 2(-2) \to 2(-2) \to \ldots$$$
$$$1(1) \to 3(1) \to 4(1) \to 1(1) \to \ldots$$$
$$$1(5) \to 3(5) \to 1(5) \to \ldots$$$

The second example is same as the first example, except that the vertices have non-zero values. Therefore the answers to the queries also differ from the first example.

$\text{[math]}$

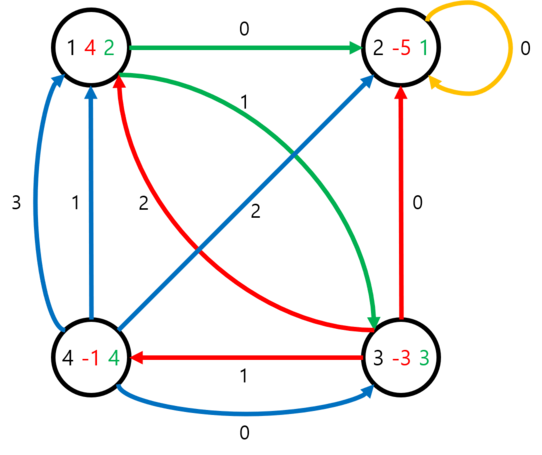
The queries for the second example works as follows:

$$$1(4) \to 2(-1) \to 2(-6) \to \ldots$$$
$$$2(-5) \to 2(-10) \to \ldots$$$
$$$3(-4) \to 1(0) \to 2(-5) \to 2(-10) \to \ldots$$$
$$$4(-3) \to 1(1) \to 3(-2) \to 4(-3) \to \ldots$$$
$$$1(5) \to 3(2) \to 1(6) \to 2(1) \to 2(-4) \to \ldots$$$
$$$1(9) \to 3(6) \to 2(1) \to 2(-4) \to \ldots$$$

Informação

Provedor Codeforces

Código CF1200F