Path Queries

Description:

Input:

The first line of the input contains two integers $$$n$$$ and $$$m$$$ ($$$1 \le n, m \le 2 \cdot 10^5$$$) — the number of vertices in the tree and the number of queries.

Each of the next $$$n - 1$$$ lines describes an edge of the tree. Edge $$$i$$$ is denoted by three integers $$$u_i$$$, $$$v_i$$$ and $$$w_i$$$ — the labels of vertices it connects ($$$1 \le u_i, v_i \le n$$$, $$$u_i \ne v_i$$$) and the weight of the edge ($$$1 \le w_i \le 2 \cdot 10^5$$$). It is guaranteed that the given edges form a tree.

The last line of the input contains $$$m$$$ integers $$$q_1, q_2, \dots, q_m$$$ ($$$1 \le q_i \le 2 \cdot 10^5$$$), where $$$q_i$$$ is the maximum weight of an edge in the $$$i$$$-th query.

Output:

Print $$$m$$$ integers — the answers to the queries. The $$$i$$$-th value should be equal to the number of pairs of vertices $$$(u, v)$$$ ($$$u < v$$$) such that the maximum weight of an edge on a simple path between $$$u$$$ and $$$v$$$ doesn't exceed $$$q_i$$$.

Queries are numbered from $$$1$$$ to $$$m$$$ in the order of the input.

Sample Input:

7 5
1 2 1
3 2 3
2 4 1
4 5 2
5 7 4
3 6 2
5 2 3 4 1

Sample Output:

21 7 15 21 3 

Sample Input:

1 2
1 2

Sample Output:

0 0 

Sample Input:

3 3
1 2 1
2 3 2
1 3 2

Sample Output:

1 3 3 

Note:

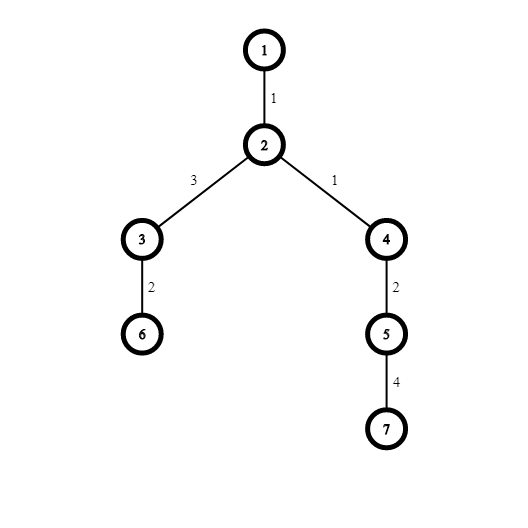
The picture shows the tree from the first example: