Hyakugoku and Ladders

1000ms

262144K

Description:

Hyakugoku has just retired from being the resident deity of the South Black Snail Temple in order to pursue her dream of becoming a cartoonist. She spent six months in that temple just playing "Cat's Cradle" so now she wants to try a different game — "Snakes and Ladders". Unfortunately, she already killed all the snakes, so there are only ladders left now.

The game is played on a $$$10 \times 10$$$ board as follows:

At the beginning of the game, the player is at the bottom left square.
The objective of the game is for the player to reach the Goal (the top left square) by following the path and climbing vertical ladders. Once the player reaches the Goal, the game ends.
The path is as follows: if a square is not the end of its row, it leads to the square next to it along the direction of its row; if a square is the end of its row, it leads to the square above it. The direction of a row is determined as follows: the direction of the bottom row is to the right; the direction of any other row is opposite the direction of the row below it. See Notes section for visualization of path.
During each turn, the player rolls a standard six-sided dice. Suppose that the number shown on the dice is $$$r$$$. If the Goal is less than $$$r$$$ squares away on the path, the player doesn't move (but the turn is performed). Otherwise, the player advances exactly $$$r$$$ squares along the path and then stops. If the player stops on a square with the bottom of a ladder, the player chooses whether or not to climb up that ladder. If she chooses not to climb, then she stays in that square for the beginning of the next turn.
Some squares have a ladder in them. Ladders are only placed vertically — each one leads to the same square of some of the upper rows. In order for the player to climb up a ladder, after rolling the dice, she must stop at the square containing the bottom of the ladder. After using the ladder, the player will end up in the square containing the top of the ladder. She cannot leave the ladder in the middle of climbing. And if the square containing the top of the ladder also contains the bottom of another ladder, she is not allowed to use that second ladder.
The numbers on the faces of the dice are 1, 2, 3, 4, 5, and 6, with each number having the same probability of being shown.

Please note that:

it is possible for ladders to overlap, but the player cannot switch to the other ladder while in the middle of climbing the first one;
it is possible for ladders to go straight to the top row, but not any higher;
it is possible for two ladders to lead to the same tile;
it is possible for a ladder to lead to a tile that also has a ladder, but the player will not be able to use that second ladder if she uses the first one;
the player can only climb up ladders, not climb down.

Hyakugoku wants to finish the game as soon as possible. Thus, on each turn she chooses whether to climb the ladder or not optimally. Help her to determine the minimum expected number of turns the game will take.

Input:

Input will consist of ten lines. The $$$i$$$-th line will contain 10 non-negative integers $$$h_{i1}, h_{i2}, \dots, h_{i10}$$$. If $$$h_{ij}$$$ is $$$0$$$, then the tile at the $$$i$$$-th row and $$$j$$$-th column has no ladder. Otherwise, the ladder at that tile will have a height of $$$h_{ij}$$$, i.e. climbing it will lead to the tile $$$h_{ij}$$$ rows directly above. It is guaranteed that $$$0 \leq h_{ij} < i$$$. Also, the first number of the first line and the first number of the last line always contain $$$0$$$, i.e. the Goal and the starting tile never have ladders.

Output:

Print only one line containing a single floating-point number — the minimum expected number of turns Hyakugoku can take to finish the game. Your answer will be considered correct if its absolute or relative error does not exceed $$$10^{-6}$$$.

Sample Input:

0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0

Sample Output:

33.0476190476

Sample Input:

0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 3 0 0 0 4 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 4 0 0 0
0 0 3 0 0 0 0 0 0 0
0 0 4 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 9

Sample Output:

20.2591405923

Sample Input:

0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 6 6 6 6 6 6 0 0 0
1 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0

Sample Output:

15.9047592939

Note:

A visualization of the path and the board from example 2 is as follows: 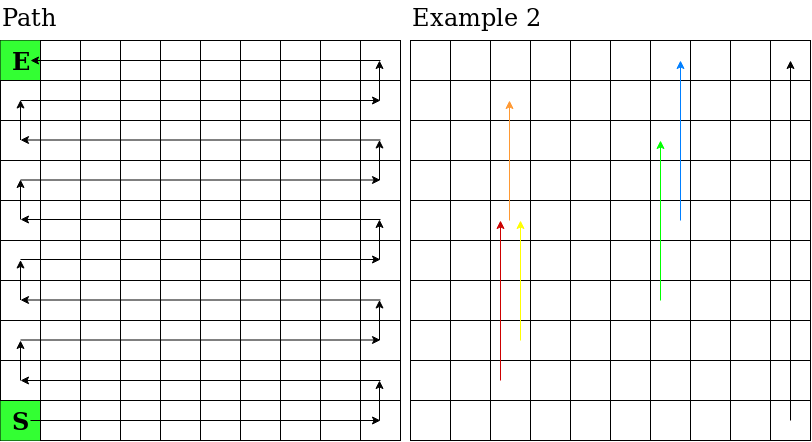$\text{[math]}$

The tile with an 'S' is the starting tile and the tile with an 'E' is the Goal.

For the first example, there are no ladders.

For the second example, the board looks like the one in the right part of the image (the ladders have been colored for clarity).

It is possible for ladders to overlap, as is the case with the red and yellow ladders and green and blue ladders. It is also possible for ladders to go straight to the top, as is the case with the black and blue ladders. However, it is not possible for ladders to go any higher (outside of the board). It is also possible that two ladders lead to the same tile, as is the case with the red and yellow ladders. Also, notice that the red and yellow ladders lead to the tile with the orange ladder. So if the player chooses to climb either of the red and yellow ladders, they will not be able to climb the orange ladder. Finally, notice that the green ladder passes through the starting tile of the blue ladder. The player cannot transfer from the green ladder to the blue ladder while in the middle of climbing the green ladder.

Informação

Provedor Codeforces

Código CF1245E