Preparando MOJI
Gardener Alexey teaches competitive programming to high school students. To congratulate Alexey on the Teacher's Day, the students have gifted him a collection of wooden sticks, where every stick has an integer length. Now Alexey wants to grow a tree from them.
The tree looks like a polyline on the plane, consisting of all sticks. The polyline starts at the point $$$(0, 0)$$$. While constructing the polyline, Alexey will attach sticks to it one by one in arbitrary order. Each stick must be either vertical or horizontal (that is, parallel to $$$OX$$$ or $$$OY$$$ axis). It is not allowed for two consecutive sticks to be aligned simultaneously horizontally or simultaneously vertically. See the images below for clarification.
Alexey wants to make a polyline in such a way that its end is as far as possible from $$$(0, 0)$$$. Please help him to grow the tree this way.
Note that the polyline defining the form of the tree may have self-intersections and self-touches, but it can be proved that the optimal answer does not contain any self-intersections or self-touches.
The first line contains an integer $$$n$$$ ($$$1 \le n \le 100\,000$$$) — the number of sticks Alexey got as a present.
The second line contains $$$n$$$ integers $$$a_1, \ldots, a_n$$$ ($$$1 \le a_i \le 10\,000$$$) — the lengths of the sticks.
Print one integer — the square of the largest possible distance from $$$(0, 0)$$$ to the tree end.
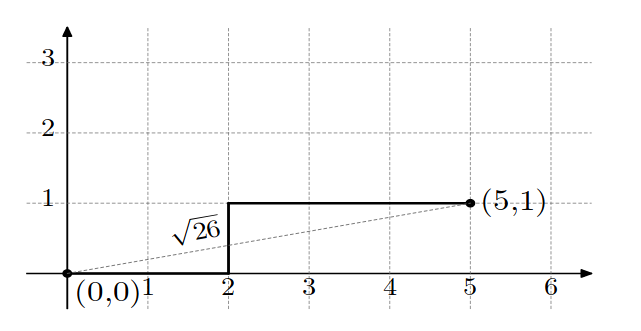
3 1 2 3
26
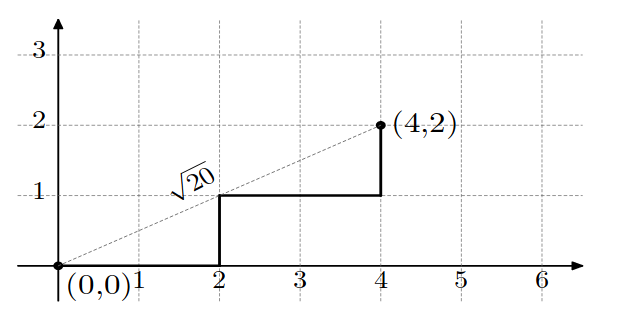
4 1 1 2 2
20
The following pictures show optimal trees for example tests. The squared distance in the first example equals $$$5 \cdot 5 + 1 \cdot 1 = 26$$$, and in the second example $$$4 \cdot 4 + 2 \cdot 2 = 20$$$.