Cheap Robot

Description:

Input:

The first line contains four integers $$$n$$$, $$$m$$$, $$$k$$$ and $$$q$$$ ($$$2 \le k \le n \le 10^5$$$ and $$$1 \le m, q \le 3 \cdot 10^5$$$).

The $$$i$$$-th of the next $$$m$$$ lines contains three integers $$$u_i$$$, $$$v_i$$$ and $$$w_i$$$ ($$$1 \le u_i, v_i \le n$$$, $$$u_i \neq v_i$$$, $$$1 \le w_i \le 10^9$$$), that mean that there's an edge between nodes $$$u$$$ and $$$v$$$, with a weight $$$w_i$$$.

It is guaranteed that the given graph is simple (there is no self-loop, and there is at most one edge between every pair of nodes) and connected.

The $$$i$$$-th of the next $$$q$$$ lines contains two integers $$$a_i$$$ and $$$b_i$$$ ($$$1 \le a_i, b_i \le k$$$, $$$a_i \neq b_i$$$).

Output:

You have to output $$$q$$$ lines, where the $$$i$$$-th line contains a single integer : the minimum capacity required to acheive the $$$i$$$-th mission.

Sample Input:

10 9 3 1
10 9 11
9 2 37
2 4 4
4 1 8
1 5 2
5 7 3
7 3 2
3 8 4
8 6 13
2 3

Sample Output:

12

Sample Input:

9 11 3 2
1 3 99
1 4 5
4 5 3
5 6 3
6 4 11
6 7 21
7 2 6
7 8 4
8 9 3
9 2 57
9 3 2
3 1
2 3

Sample Output:

38
15

Note:

In the first example, the graph is the chain $$$10 - 9 - 2^C - 4 - 1^C - 5 - 7 - 3^C - 8 - 6$$$, where centrals are nodes $$$1$$$, $$$2$$$ and $$$3$$$.

For the mission $$$(2, 3)$$$, there is only one simple path possible. Here is a simulation of this mission when the capacity is $$$12$$$.

• The robot begins on the node $$$2$$$, with $$$c = 12$$$ energy points.
• The robot uses an edge of weight $$$4$$$.
• The robot reaches the node $$$4$$$, with $$$12 - 4 = 8$$$ energy points.
• The robot uses an edge of weight $$$8$$$.
• The robot reaches the node $$$1$$$ with $$$8 - 8 = 0$$$ energy points.
• The robot is on a central, so its battery is recharged. He has now $$$c = 12$$$ energy points.
• The robot uses an edge of weight $$$2$$$.
• The robot is on the node $$$5$$$, with $$$12 - 2 = 10$$$ energy points.
• The robot uses an edge of weight $$$3$$$.
• The robot is on the node $$$7$$$, with $$$10 - 3 = 7$$$ energy points.
• The robot uses an edge of weight $$$2$$$.
• The robot is on the node $$$3$$$, with $$$7 - 2 = 5$$$ energy points.
• The robot is on a central, so its battery is recharged. He has now $$$c = 12$$$ energy points.
• End of the simulation.

Note that if value of $$$c$$$ was lower than $$$12$$$, we would have less than $$$8$$$ energy points on node $$$4$$$, and we would be unable to use the edge $$$4 \leftrightarrow 1$$$ of weight $$$8$$$. Hence $$$12$$$ is the minimum capacity required to acheive the mission.

—

The graph of the second example is described here (centrals are red nodes):

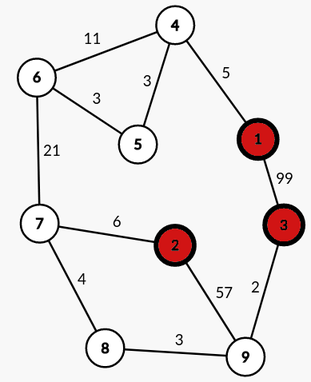
The robot can acheive the mission $$$(3, 1)$$$ with a battery of capacity $$$c = 38$$$, using the path $$$3 \rightarrow 9 \rightarrow 8 \rightarrow 7 \rightarrow 2 \rightarrow 7 \rightarrow 6 \rightarrow 5 \rightarrow 4 \rightarrow 1$$$

The robot can acheive the mission $$$(2, 3)$$$ with a battery of capacity $$$c = 15$$$, using the path $$$2 \rightarrow 7 \rightarrow 8 \rightarrow 9 \rightarrow 3$$$