Preparando MOJI
This is an interactive problem.
Khanh has $$$n$$$ points on the Cartesian plane, denoted by $$$a_1, a_2, \ldots, a_n$$$. All points' coordinates are integers between $$$-10^9$$$ and $$$10^9$$$, inclusive. No three points are collinear. He says that these points are vertices of a convex polygon; in other words, there exists a permutation $$$p_1, p_2, \ldots, p_n$$$ of integers from $$$1$$$ to $$$n$$$ such that the polygon $$$a_{p_1} a_{p_2} \ldots a_{p_n}$$$ is convex and vertices are listed in counter-clockwise order.
Khanh gives you the number $$$n$$$, but hides the coordinates of his points. Your task is to guess the above permutation by asking multiple queries. In each query, you give Khanh $$$4$$$ integers $$$t$$$, $$$i$$$, $$$j$$$, $$$k$$$; where either $$$t = 1$$$ or $$$t = 2$$$; and $$$i$$$, $$$j$$$, $$$k$$$ are three distinct indices from $$$1$$$ to $$$n$$$, inclusive. In response, Khanh tells you:
Recall that the cross product of vector $$$\overrightarrow{a} = (x_a, y_a)$$$ and vector $$$\overrightarrow{b} = (x_b, y_b)$$$ is the integer $$$x_a \cdot y_b - x_b \cdot y_a$$$. The sign of a number is $$$1$$$ it it is positive, and $$$-1$$$ otherwise. It can be proven that the cross product obtained in the above queries can not be $$$0$$$.
You can ask at most $$$3 \cdot n$$$ queries.
Please note that Khanh fixes the coordinates of his points and does not change it while answering your queries. You do not need to guess the coordinates. In your permutation $$$a_{p_1}a_{p_2}\ldots a_{p_n}$$$, $$$p_1$$$ should be equal to $$$1$$$ and the indices of vertices should be listed in counter-clockwise order.
You start the interaction by reading $$$n$$$ ($$$3 \leq n \leq 1\,000$$$) — the number of vertices.
To ask a query, write $$$4$$$ integers $$$t$$$, $$$i$$$, $$$j$$$, $$$k$$$ ($$$1 \leq t \leq 2$$$, $$$1 \leq i, j, k \leq n$$$) in a separate line. $$$i$$$, $$$j$$$ and $$$k$$$ should be distinct.
Then read a single integer to get the answer to this query, as explained above. It can be proven that the answer of a query is always an integer.
When you find the permutation, write a number $$$0$$$. Then write $$$n$$$ integers $$$p_1, p_2, \ldots, p_n$$$ in the same line.
After printing a query do not forget to output end of line and flush the output. Otherwise, you will get Idleness limit exceeded. To do this, use:
Hack format
To hack, use the following format:
The first line contains an integer $$$n$$$ ($$$3 \leq n \leq 1\,000$$$) — the number of vertices.
The $$$i$$$-th of the next $$$n$$$ lines contains two integers $$$x_i$$$ and $$$y_i$$$ ($$$-10^9 \le x_i, y_i \le 10^9$$$) — the coordinate of the point $$$a_i$$$.
6 15 -1 1
1 1 4 6 2 1 5 6 2 2 1 4 0 1 3 4 2 6 5
The image below shows the hidden polygon in the example:
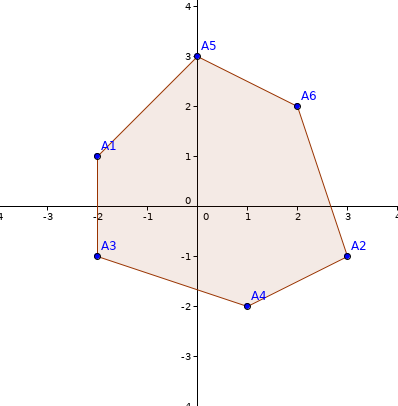
The interaction in the example goes as below: