Tree Queries

Description:

Input:

The first line contains two integers $$$n$$$ and $$$q$$$ ($$$1 \leq n, q \leq 150\,000$$$) — the number of vertices on Hanh's tree and the number of operations he performs.

Each of the next $$$n - 1$$$ lines contains two integers $$$u$$$ and $$$v$$$ ($$$1 \leq u, v \leq n$$$), denoting that there is an edge connecting two vertices $$$u$$$ and $$$v$$$. It is guaranteed that these $$$n - 1$$$ edges form a tree.

Each of the last $$$q$$$ lines describes an operation in either formats:

• $$$1$$$ $$$v$$$ $$$d$$$ ($$$1 \leq v \leq n, 0 \leq d \leq 10^7$$$), representing a first-type operation.
• $$$2$$$ $$$v$$$ ($$$1 \leq v \leq n$$$), representing a second-type operation.

It is guaranteed that there is at least one query of the second type.

Output:

For each operation of the second type, write the expected value on a single line.

Let $$$M = 998244353$$$, it can be shown that the expected value can be expressed as an irreducible fraction $$$\frac{p}{q}$$$, where $$$p$$$ and $$$q$$$ are integers and $$$q \not \equiv 0 \pmod{M}$$$. Output the integer equal to $$$p \cdot q^{-1} \bmod M$$$. In other words, output such an integer $$$x$$$ that $$$0 \le x < M$$$ and $$$x \cdot q \equiv p \pmod{M}$$$.

Sample Input:

5 12
1 2
1 3
2 4
2 5
1 1 1
2 1
2 2
2 3
2 4
2 5
1 2 2
2 1
2 2
2 3
2 4
2 5

Sample Output:

1
199648871
399297742
199648871
199648871
598946614
199648873
2
2
2

Note:

The image below shows the tree in the example:

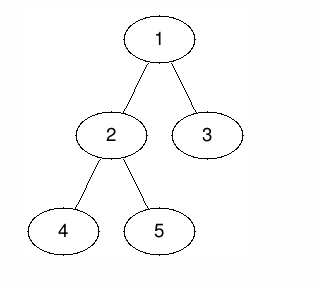
For the first query, where $$$v = 1$$$ and $$$d = 1$$$:

• If $$$r = 1$$$, the values of all vertices get increased.
• If $$$r = 2$$$, the values of vertices $$$1$$$ and $$$3$$$ get increased.
• If $$$r = 3$$$, the values of vertices $$$1$$$, $$$2$$$, $$$4$$$ and $$$5$$$ get increased.
• If $$$r = 4$$$, the values of vertices $$$1$$$ and $$$3$$$ get increased.
• If $$$r = 5$$$, the values of vertices $$$1$$$ and $$$3$$$ get increased.

Hence, the expected values of all vertices after this query are ($$$1, 0.4, 0.8, 0.4, 0.4$$$).

For the second query, where $$$v = 2$$$ and $$$d = 2$$$:

• If $$$r = 1$$$, the values of vertices $$$2$$$, $$$4$$$ and $$$5$$$ get increased.
• If $$$r = 2$$$, the values of all vertices get increased.
• If $$$r = 3$$$, the values of vertices $$$2$$$, $$$4$$$ and $$$5$$$ get increased.
• If $$$r = 4$$$, the values of vertices $$$1$$$, $$$2$$$, $$$3$$$ and $$$5$$$ get increased.
• If $$$r = 5$$$, the values of vertices $$$1$$$, $$$2$$$, $$$3$$$ and $$$4$$$ get increased.

Hence, the expected values of all vertices after this query are ($$$2.2, 2.4, 2, 2, 2$$$).