Preparando MOJI
There is given an integer $$$k$$$ and a grid $$$2^k \times 2^k$$$ with some numbers written in its cells, cell $$$(i, j)$$$ initially contains number $$$a_{ij}$$$. Grid is considered to be a torus, that is, the cell to the right of $$$(i, 2^k)$$$ is $$$(i, 1)$$$, the cell below the $$$(2^k, i)$$$ is $$$(1, i)$$$ There is also given a lattice figure $$$F$$$, consisting of $$$t$$$ cells, where $$$t$$$ is odd. $$$F$$$ doesn't have to be connected.
We can perform the following operation: place $$$F$$$ at some position on the grid. (Only translations are allowed, rotations and reflections are prohibited). Now choose any nonnegative integer $$$p$$$. After that, for each cell $$$(i, j)$$$, covered by $$$F$$$, replace $$$a_{ij}$$$ by $$$a_{ij}\oplus p$$$, where $$$\oplus$$$ denotes the bitwise XOR operation.
More formally, let $$$F$$$ be given by cells $$$(x_1, y_1), (x_2, y_2), \dots, (x_t, y_t)$$$. Then you can do the following operation: choose any $$$x, y$$$ with $$$1\le x, y \le 2^k$$$, any nonnegative integer $$$p$$$, and for every $$$i$$$ from $$$1$$$ to $$$n$$$ replace number in the cell $$$(((x + x_i - 1)\bmod 2^k) + 1, ((y + y_i - 1)\bmod 2^k) + 1)$$$ with $$$a_{((x + x_i - 1)\bmod 2^k) + 1, ((y + y_i - 1)\bmod 2^k) + 1}\oplus p$$$.
Our goal is to make all the numbers equal to $$$0$$$. Can we achieve it? If we can, find the smallest number of operations in which it is possible to do this.
The first line contains a single integer $$$k$$$ ($$$1 \le k \le 9$$$).
The $$$i$$$-th of the next $$$2^k$$$ lines contains $$$2^k$$$ integers $$$a_{i1}, a_{i2}, \dots, a_{i2^k}$$$ ($$$0 \le a_{ij} < 2^{60}$$$) — initial values in the $$$i$$$-th row of the grid.
The next line contains a single integer $$$t$$$ ($$$1\le t \le \min(99, 4^k)$$$, $$$t$$$ is odd) — number of cells of figure.
$$$i$$$-th of next $$$t$$$ lines contains two integers $$$x_i$$$ and $$$y_i$$$ ($$$1 \le x_i, y_i \le 2^k$$$), describing the position of the $$$i$$$-th cell of the figure.
It is guaranteed that all cells are different, but it is not guaranteed that the figure is connected.
If it is impossible to make all numbers in the grid equal to $$$0$$$ with these operations, output $$$-1$$$.
Otherwise, output a single integer — the minimal number of operations needed to do this. It can be shown that if it is possible to make all numbers equal $$$0$$$, it is possible to do so in less than $$$10^{18}$$$ operations.
2 5 5 5 5 2 6 2 3 0 0 2 0 0 0 0 0 5 1 1 1 2 1 3 1 4 2 4
3
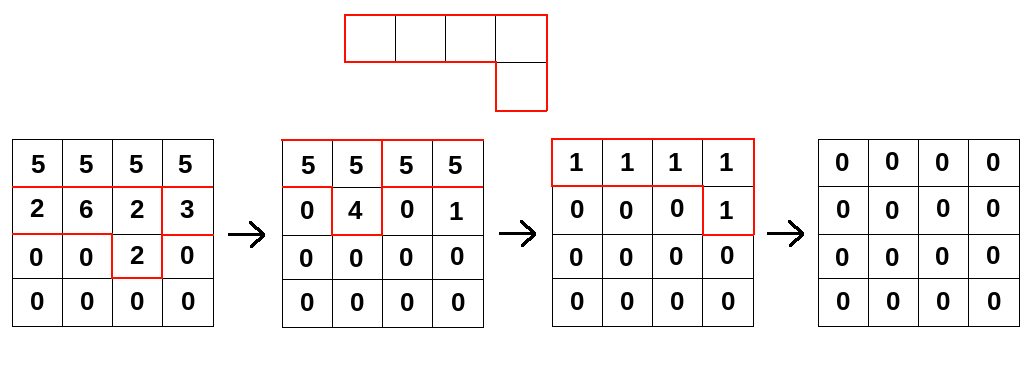
The figure and the operations for the example are shown above:
Informação
Provedor Codeforces
Código CF1270I
Tags
Submetido 0
BOUA! 0
Taxa de BOUA's 0%
Datas 09/05/2023 09:57:05
Relacionados