Preparando MOJI
You are given a rectangular matrix of size $$$n \times m$$$ consisting of integers from $$$1$$$ to $$$2 \cdot 10^5$$$.
In one move, you can:
A cyclic shift is an operation such that you choose some $$$j$$$ ($$$1 \le j \le m$$$) and set $$$a_{1, j} := a_{2, j}, a_{2, j} := a_{3, j}, \dots, a_{n, j} := a_{1, j}$$$ simultaneously.
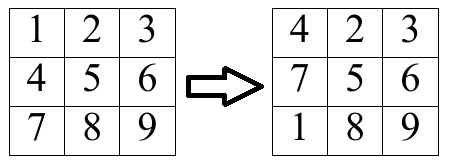Example of cyclic shift of the first column You want to perform the minimum number of moves to make this matrix look like this:
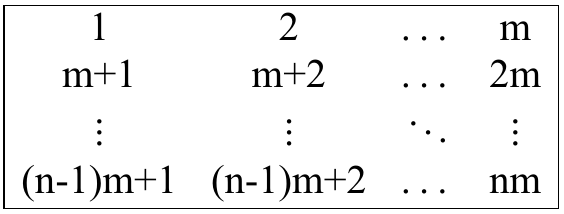
In other words, the goal is to obtain the matrix, where $$$a_{1, 1} = 1, a_{1, 2} = 2, \dots, a_{1, m} = m, a_{2, 1} = m + 1, a_{2, 2} = m + 2, \dots, a_{n, m} = n \cdot m$$$ (i.e. $$$a_{i, j} = (i - 1) \cdot m + j$$$) with the minimum number of moves performed.
The first line of the input contains two integers $$$n$$$ and $$$m$$$ ($$$1 \le n, m \le 2 \cdot 10^5, n \cdot m \le 2 \cdot 10^5$$$) — the size of the matrix.
The next $$$n$$$ lines contain $$$m$$$ integers each. The number at the line $$$i$$$ and position $$$j$$$ is $$$a_{i, j}$$$ ($$$1 \le a_{i, j} \le 2 \cdot 10^5$$$).
Print one integer — the minimum number of moves required to obtain the matrix, where $$$a_{1, 1} = 1, a_{1, 2} = 2, \dots, a_{1, m} = m, a_{2, 1} = m + 1, a_{2, 2} = m + 2, \dots, a_{n, m} = n \cdot m$$$ ($$$a_{i, j} = (i - 1)m + j$$$).
3 3 3 2 1 1 2 3 4 5 6
6
4 3 1 2 3 4 5 6 7 8 9 10 11 12
0
3 4 1 6 3 4 5 10 7 8 9 2 11 12
2
In the first example, you can set $$$a_{1, 1} := 7, a_{1, 2} := 8$$$ and $$$a_{1, 3} := 9$$$ then shift the first, the second and the third columns cyclically, so the answer is $$$6$$$. It can be shown that you cannot achieve a better answer.
In the second example, the matrix is already good so the answer is $$$0$$$.
In the third example, it is enough to shift the second column cyclically twice to obtain a good matrix, so the answer is $$$2$$$.
Informação
Provedor Codeforces
Código CF1294E
Tags
Submetido 0
BOUA! 0
Taxa de BOUA's 0%
Datas 09/05/2023 09:58:29
Relacionados