Preparando MOJI
Guy-Manuel and Thomas are going to build a polygon spaceship.
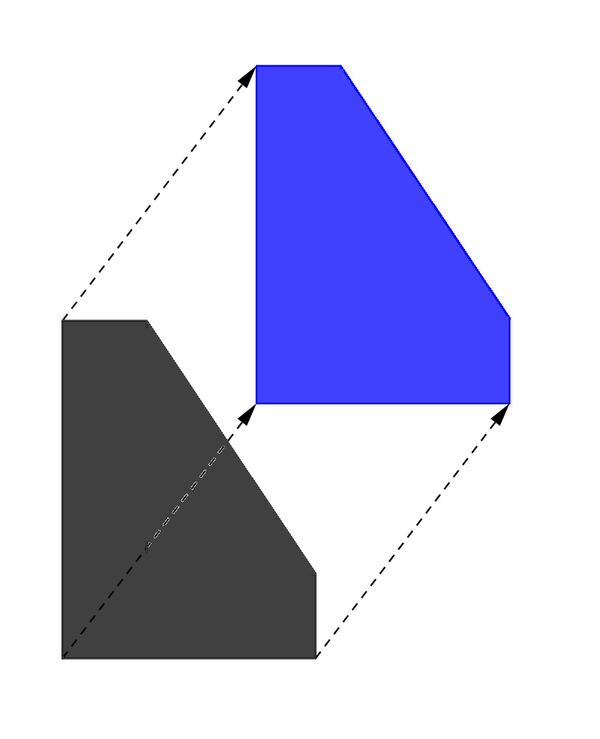
You're given a strictly convex (i. e. no three points are collinear) polygon $$$P$$$ which is defined by coordinates of its vertices. Define $$$P(x,y)$$$ as a polygon obtained by translating $$$P$$$ by vector $$$\overrightarrow {(x,y)}$$$. The picture below depicts an example of the translation:
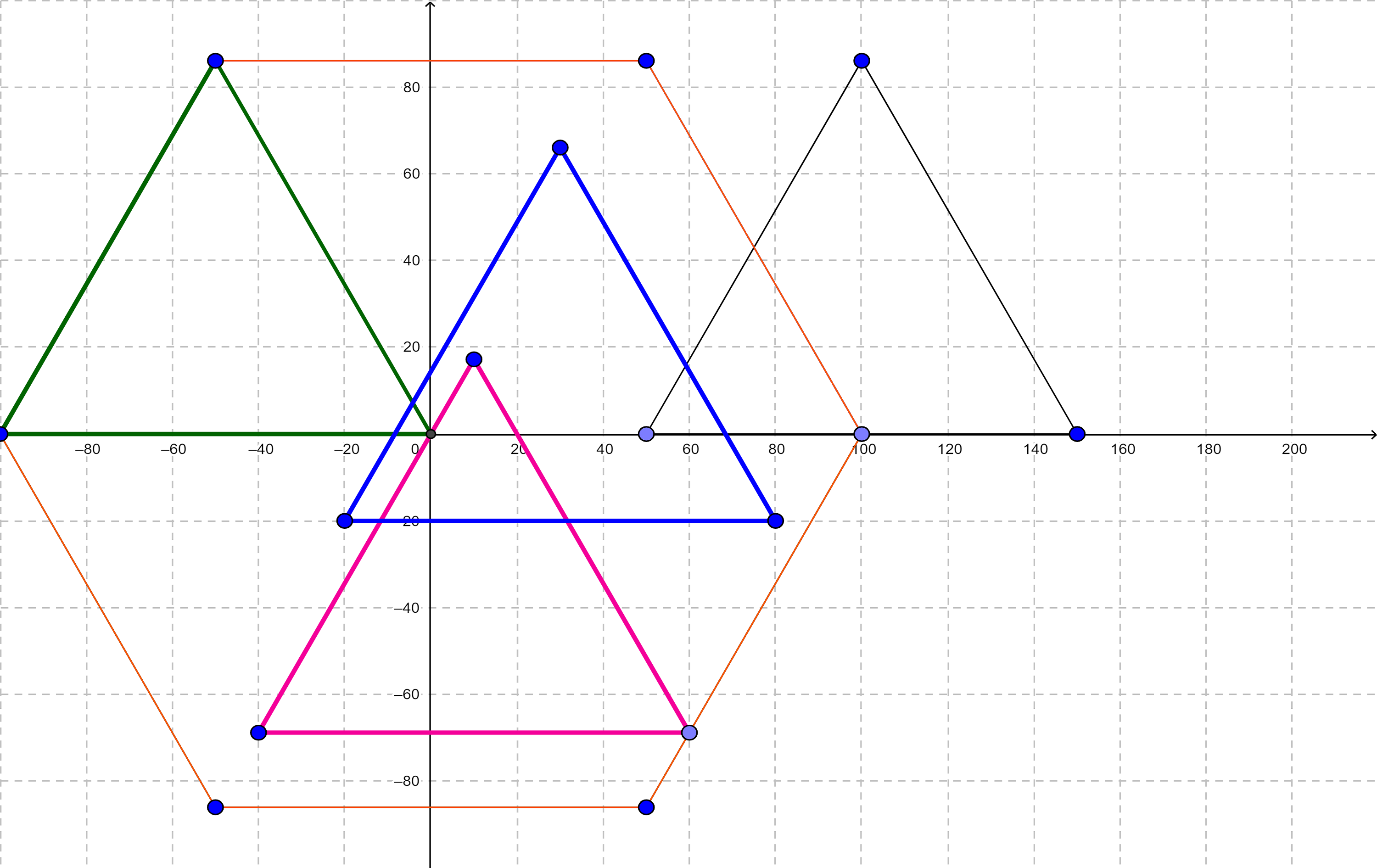
Define $$$T$$$ as a set of points which is the union of all $$$P(x,y)$$$ such that the origin $$$(0,0)$$$ lies in $$$P(x,y)$$$ (both strictly inside and on the boundary). There is also an equivalent definition: a point $$$(x,y)$$$ lies in $$$T$$$ only if there are two points $$$A,B$$$ in $$$P$$$ such that $$$\overrightarrow {AB} = \overrightarrow {(x,y)}$$$. One can prove $$$T$$$ is a polygon too. For example, if $$$P$$$ is a regular triangle then $$$T$$$ is a regular hexagon. At the picture below $$$P$$$ is drawn in black and some $$$P(x,y)$$$ which contain the origin are drawn in colored:
The spaceship has the best aerodynamic performance if $$$P$$$ and $$$T$$$ are similar. Your task is to check whether the polygons $$$P$$$ and $$$T$$$ are similar.
The first line of input will contain a single integer $$$n$$$ ($$$3 \le n \le 10^5$$$) — the number of points.
The $$$i$$$-th of the next $$$n$$$ lines contains two integers $$$x_i, y_i$$$ ($$$|x_i|, |y_i| \le 10^9$$$), denoting the coordinates of the $$$i$$$-th vertex.
It is guaranteed that these points are listed in counterclockwise order and these points form a strictly convex polygon.
Output "YES" in a separate line, if $$$P$$$ and $$$T$$$ are similar. Otherwise, output "NO" in a separate line. You can print each letter in any case (upper or lower).
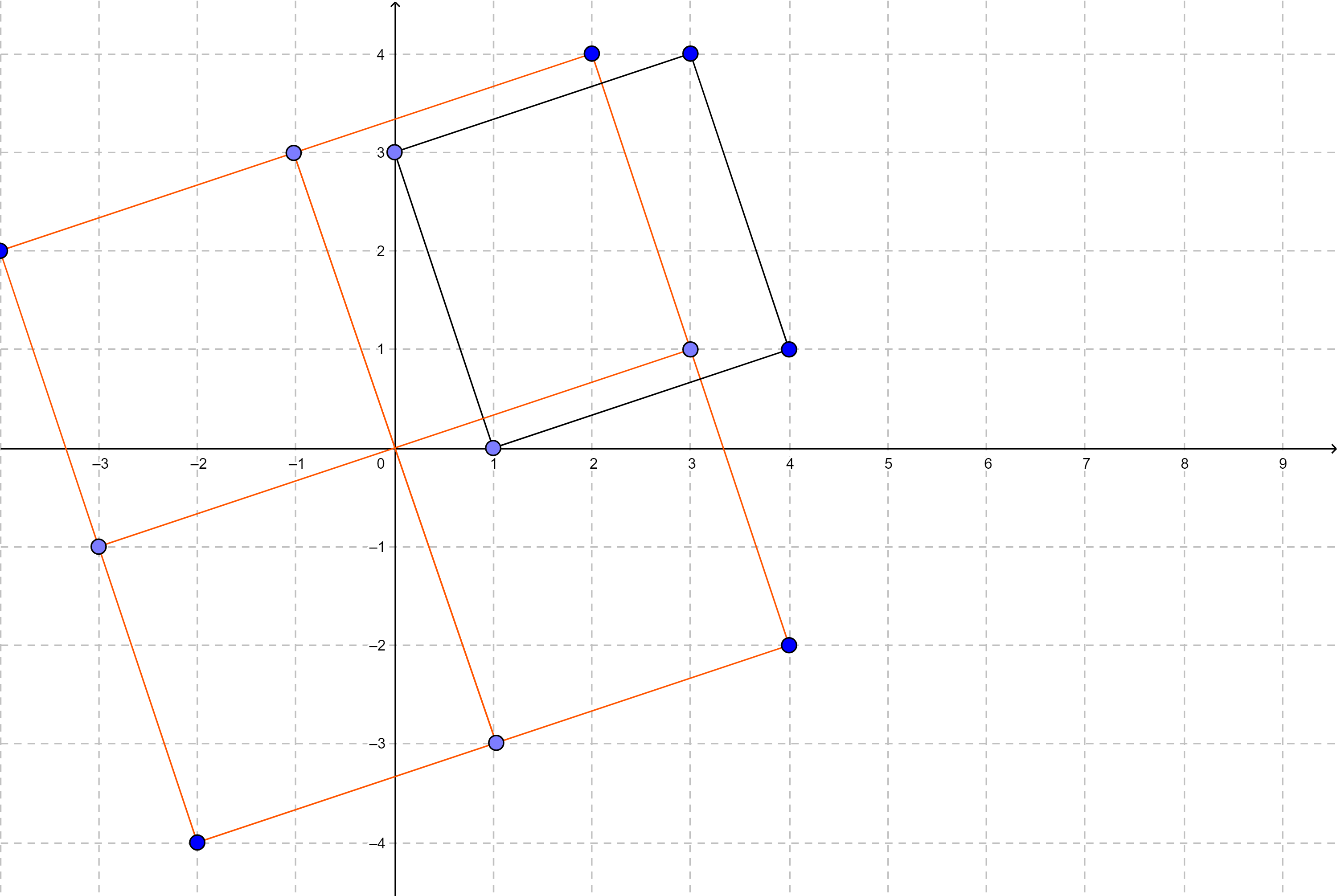
4 1 0 4 1 3 4 0 3
YES
3 100 86 50 0 150 0
nO
8 0 0 1 0 2 1 3 3 4 6 3 6 2 5 1 3
YES
The following image shows the first sample: both $$$P$$$ and $$$T$$$ are squares. The second sample was shown in the statements.
Informação
Provedor Codeforces
Código CF1299B
Tags
Submetido 0
BOUA! 0
Taxa de BOUA's 0%
Datas 09/05/2023 09:58:48
Relacionados