Maximum White Subtree

Description:

Input:

The first line of the input contains one integer $$$n$$$ ($$$2 \le n \le 2 \cdot 10^5$$$) — the number of vertices in the tree.

The second line of the input contains $$$n$$$ integers $$$a_1, a_2, \dots, a_n$$$ ($$$0 \le a_i \le 1$$$), where $$$a_i$$$ is the color of the $$$i$$$-th vertex.

Each of the next $$$n-1$$$ lines describes an edge of the tree. Edge $$$i$$$ is denoted by two integers $$$u_i$$$ and $$$v_i$$$, the labels of vertices it connects $$$(1 \le u_i, v_i \le n, u_i \ne v_i$$$).

It is guaranteed that the given edges form a tree.

Output:

Print $$$n$$$ integers $$$res_1, res_2, \dots, res_n$$$, where $$$res_i$$$ is the maximum possible difference between the number of white and black vertices in some subtree that contains the vertex $$$i$$$.

Sample Input:

9
0 1 1 1 0 0 0 0 1
1 2
1 3
3 4
3 5
2 6
4 7
6 8
5 9

Sample Output:

2 2 2 2 2 1 1 0 2 

Sample Input:

4
0 0 1 0
1 2
1 3
1 4

Sample Output:

0 -1 1 -1 

Note:

The first example is shown below:

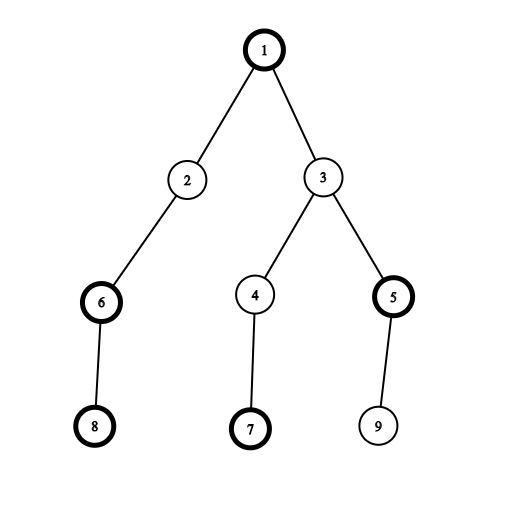
The black vertices have bold borders.

In the second example, the best subtree for vertices $$$2, 3$$$ and $$$4$$$ are vertices $$$2, 3$$$ and $$$4$$$ correspondingly. And the best subtree for the vertex $$$1$$$ is the subtree consisting of vertices $$$1$$$ and $$$3$$$.