Preparando MOJI
You are given a tree consisting of $$$n$$$ nodes. You want to write some labels on the tree's edges such that the following conditions hold:
Here, $$$MEX(u,v)$$$ denotes the smallest non-negative integer that isn't written on any edge on the unique simple path from node $$$u$$$ to node $$$v$$$.
The first line contains the integer $$$n$$$ ($$$2 \le n \le 10^5$$$) — the number of nodes in the tree.
Each of the next $$$n-1$$$ lines contains two space-separated integers $$$u$$$ and $$$v$$$ ($$$1 \le u,v \le n$$$) that mean there's an edge between nodes $$$u$$$ and $$$v$$$. It's guaranteed that the given graph is a tree.
Output $$$n-1$$$ integers. The $$$i^{th}$$$ of them will be the number written on the $$$i^{th}$$$ edge (in the input order).
3 1 2 1 3
0 1
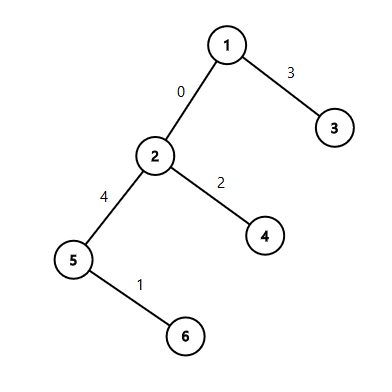
6 1 2 1 3 2 4 2 5 5 6
0 3 2 4 1
The tree from the second sample: