Divisor Paths

3000ms

262144K

Description:

You are given a positive integer $$$D$$$. Let's build the following graph from it:

each vertex is a divisor of $$$D$$$ (not necessarily prime, $$$1$$$ and $$$D$$$ itself are also included);
two vertices $$$x$$$ and $$$y$$$ ($$$x > y$$$) have an undirected edge between them if $$$x$$$ is divisible by $$$y$$$ and $$$\frac x y$$$ is a prime;
the weight of an edge is the number of divisors of $$$x$$$ that are not divisors of $$$y$$$.

For example, here is the graph for $$$D=12$$$:

$\text{[math]}$

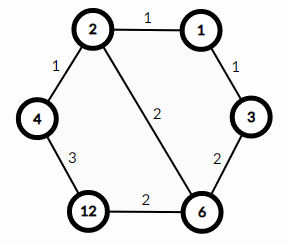
Edge $$$(4,12)$$$ has weight $$$3$$$ because $$$12$$$ has divisors $$$[1,2,3,4,6,12]$$$ and $$$4$$$ has divisors $$$[1,2,4]$$$. Thus, there are $$$3$$$ divisors of $$$12$$$ that are not divisors of $$$4$$$ — $$$[3,6,12]$$$.

There is no edge between $$$3$$$ and $$$2$$$ because $$$3$$$ is not divisible by $$$2$$$. There is no edge between $$$12$$$ and $$$3$$$ because $$$\frac{12}{3}=4$$$ is not a prime.

Let the length of the path between some vertices $$$v$$$ and $$$u$$$ in the graph be the total weight of edges on it. For example, path $$$[(1, 2), (2, 6), (6, 12), (12, 4), (4, 2), (2, 6)]$$$ has length $$$1+2+2+3+1+2=11$$$. The empty path has length $$$0$$$.

So the shortest path between two vertices $$$v$$$ and $$$u$$$ is the path that has the minimal possible length.

Two paths $$$a$$$ and $$$b$$$ are different if there is either a different number of edges in them or there is a position $$$i$$$ such that $$$a_i$$$ and $$$b_i$$$ are different edges.

You are given $$$q$$$ queries of the following form:

$$$v$$$ $$$u$$$ — calculate the number of the shortest paths between vertices $$$v$$$ and $$$u$$$.

The answer for each query might be large so print it modulo $$$998244353$$$.

Input:

The first line contains a single integer $$$D$$$ ($$$1 \le D \le 10^{15}$$$) — the number the graph is built from.

The second line contains a single integer $$$q$$$ ($$$1 \le q \le 3 \cdot 10^5$$$) — the number of queries.

Each of the next $$$q$$$ lines contains two integers $$$v$$$ and $$$u$$$ ($$$1 \le v, u \le D$$$). It is guaranteed that $$$D$$$ is divisible by both $$$v$$$ and $$$u$$$ (both $$$v$$$ and $$$u$$$ are divisors of $$$D$$$).

Output:

Print $$$q$$$ integers — for each query output the number of the shortest paths between the two given vertices modulo $$$998244353$$$.

Sample Input:

Sample Output:

1
3
1

Sample Input:

1
1
1 1

Sample Output:

Sample Input:

288807105787200
4
46 482955026400
12556830686400 897
414 12556830686400
4443186242880 325

Sample Output:

Note:

In the first example:

The first query is only the empty path — length $$$0$$$;
The second query are paths $$$[(12, 4), (4, 2), (2, 1)]$$$ (length $$$3+1+1=5$$$), $$$[(12, 6), (6, 2), (2, 1)]$$$ (length $$$2+2+1=5$$$) and $$$[(12, 6), (6, 3), (3, 1)]$$$ (length $$$2+2+1=5$$$).
The third query is only the path $$$[(3, 1), (1, 2), (2, 4)]$$$ (length $$$1+1+1=3$$$).

Informação

Provedor Codeforces

Código CF1334E