Linova and Kingdom

Description:

Input:

The first line contains two integers $$$n$$$ and $$$k$$$ ($$$2\le n\le 2 \cdot 10^5$$$, $$$1\le k< n$$$)  — the number of cities and industry cities respectively.

Each of the next $$$n-1$$$ lines contains two integers $$$u$$$ and $$$v$$$ ($$$1\le u,v\le n$$$), denoting there is a road connecting city $$$u$$$ and city $$$v$$$.

It is guaranteed that from any city, you can reach any other city by the roads.

Output:

Print the only line containing a single integer  — the maximum possible sum of happinesses of all envoys.

Sample Input:

7 4
1 2
1 3
1 4
3 5
3 6
4 7

Sample Output:

7

Sample Input:

4 1
1 2
1 3
2 4

Sample Output:

2

Sample Input:

8 5
7 5
1 7
6 1
3 7
8 3
2 1
4 5

Sample Output:

9

Note:

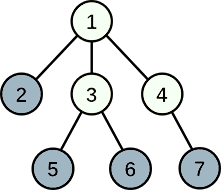
In the first example, Linova can choose cities $$$2$$$, $$$5$$$, $$$6$$$, $$$7$$$ to develop industry, then the happiness of the envoy from city $$$2$$$ is $$$1$$$, the happiness of envoys from cities $$$5$$$, $$$6$$$, $$$7$$$ is $$$2$$$. The sum of happinesses is $$$7$$$, and it can be proved to be the maximum one.

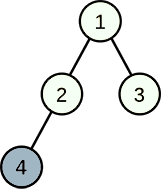
In the second example, choosing cities $$$3$$$, $$$4$$$ developing industry can reach a sum of $$$3$$$, but remember that Linova plans to choose exactly $$$k$$$ cities developing industry, then the maximum sum is $$$2$$$.