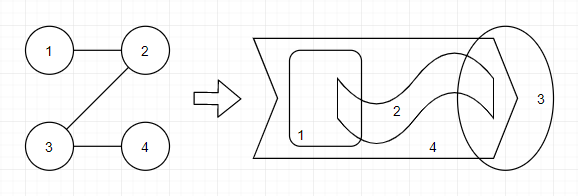
Preparando MOJI
You have a tree of $$$n$$$ vertices. You are going to convert this tree into $$$n$$$ rubber bands on infinitely large plane. Conversion rule follows:
Now let's define following things:
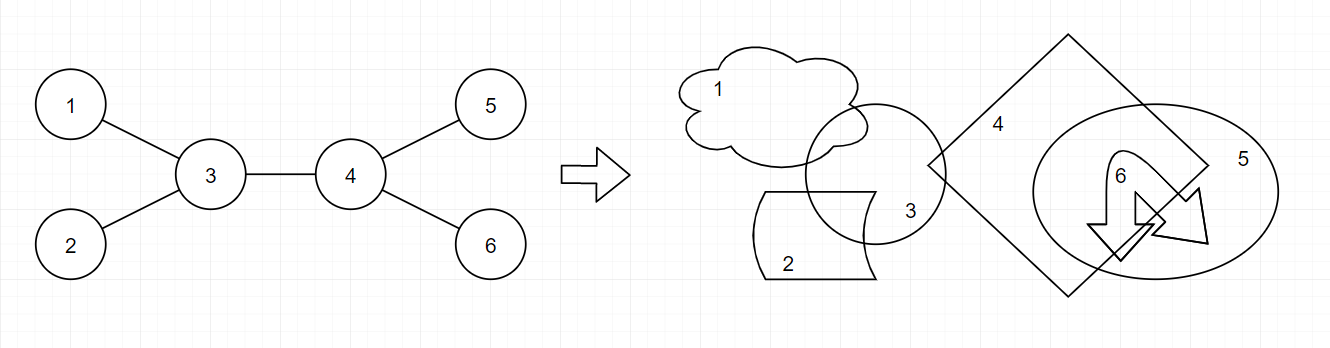 This is an example of conversion. Note that rubber bands $$$5$$$ and $$$6$$$ are nested.
This is an example of conversion. Note that rubber bands $$$5$$$ and $$$6$$$ are nested. It can be proved that is it possible to make a conversion and sequence of nested rubber bands under given constraints.
What is the maximum length of sequence of nested rubber bands can be obtained from given tree? Find and print it.
The first line contains integer $$$n$$$ ($$$3 \le n \le 10^{5}$$$) — the number of vertices in tree.
The $$$i$$$-th of the next $$$n-1$$$ lines contains two integers $$$a_{i}$$$ and $$$b_{i}$$$ ($$$1 \le a_{i} \lt b_{i} \le n$$$) — it means there is an edge between $$$a_{i}$$$ and $$$b_{i}$$$. It is guaranteed that given graph forms tree of $$$n$$$ vertices.
Print the answer.
6 1 3 2 3 3 4 4 5 4 6
4
4 1 2 2 3 3 4
2
In the first sample, you can obtain a nested sequence of $$$4$$$ rubber bands($$$1$$$, $$$2$$$, $$$5$$$, and $$$6$$$) by the conversion shown below. Of course, there are other conversions exist to make a nested sequence of $$$4$$$ rubber bands. However, you cannot make sequence of $$$5$$$ or more nested rubber bands with given tree.
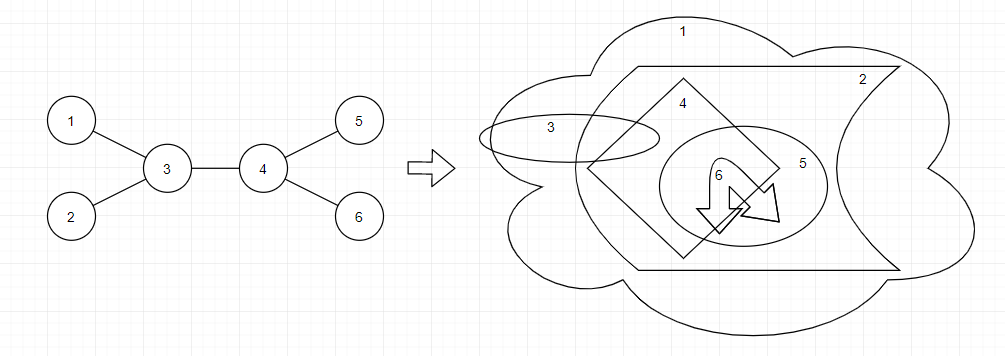
You can see one of the possible conversions for the second sample below.