Preparando MOJI
Denis, after buying flowers and sweets (you will learn about this story in the next task), went to a date with Nastya to ask her to become a couple. Now, they are sitting in the cafe and finally... Denis asks her to be together, but ... Nastya doesn't give any answer.
The poor boy was very upset because of that. He was so sad that he punched some kind of scoreboard with numbers. The numbers are displayed in the same way as on an electronic clock: each digit position consists of $$$7$$$ segments, which can be turned on or off to display different numbers. The picture shows how all $$$10$$$ decimal digits are displayed:
After the punch, some segments stopped working, that is, some segments might stop glowing if they glowed earlier. But Denis remembered how many sticks were glowing and how many are glowing now. Denis broke exactly $$$k$$$ segments and he knows which sticks are working now. Denis came up with the question: what is the maximum possible number that can appear on the board if you turn on exactly $$$k$$$ sticks (which are off now)?
It is allowed that the number includes leading zeros.
The first line contains integer $$$n$$$ $$$(1 \leq n \leq 2000)$$$ — the number of digits on scoreboard and $$$k$$$ $$$(0 \leq k \leq 2000)$$$ — the number of segments that stopped working.
The next $$$n$$$ lines contain one binary string of length $$$7$$$, the $$$i$$$-th of which encodes the $$$i$$$-th digit of the scoreboard.
Each digit on the scoreboard consists of $$$7$$$ segments. We number them, as in the picture below, and let the $$$i$$$-th place of the binary string be $$$0$$$ if the $$$i$$$-th stick is not glowing and $$$1$$$ if it is glowing. Then a binary string of length $$$7$$$ will specify which segments are glowing now.
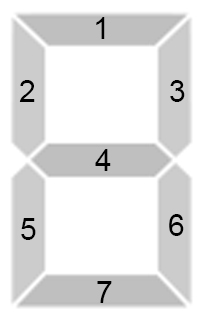
Thus, the sequences "1110111", "0010010", "1011101", "1011011", "0111010", "1101011", "1101111", "1010010", "1111111", "1111011" encode in sequence all digits from $$$0$$$ to $$$9$$$ inclusive.
Output a single number consisting of $$$n$$$ digits — the maximum number that can be obtained if you turn on exactly $$$k$$$ sticks or $$$-1$$$, if it is impossible to turn on exactly $$$k$$$ sticks so that a correct number appears on the scoreboard digits.
1 7 0000000
8
2 5 0010010 0010010
97
3 5 0100001 1001001 1010011
-1
In the first test, we are obliged to include all $$$7$$$ sticks and get one $$$8$$$ digit on the scoreboard.
In the second test, we have sticks turned on so that units are formed. For $$$5$$$ of additionally included sticks, you can get the numbers $$$07$$$, $$$18$$$, $$$34$$$, $$$43$$$, $$$70$$$, $$$79$$$, $$$81$$$ and $$$97$$$, of which we choose the maximum — $$$97$$$.
In the third test, it is impossible to turn on exactly $$$5$$$ sticks so that a sequence of numbers appears on the scoreboard.
Informação
Provedor Codeforces
Código CF1340B
Tags
Submetido 0
BOUA! 0
Taxa de BOUA's 0%
Datas 09/05/2023 10:01:28
Relacionados