Preparando MOJI
Lee is going to fashionably decorate his house for a party, using some regular convex polygons...
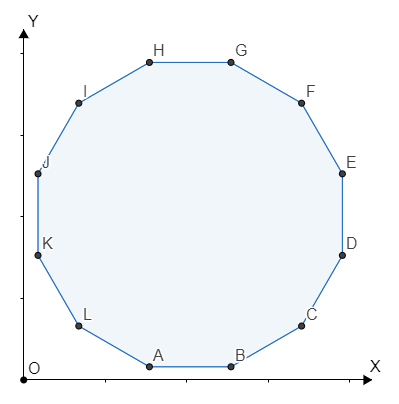
Lee thinks a regular $$$n$$$-sided (convex) polygon is beautiful if and only if he can rotate it in such a way that at least one of its edges is parallel to the $$$OX$$$-axis and at least one of its edges is parallel to the $$$OY$$$-axis at the same time.
Recall that a regular $$$n$$$-sided polygon is a convex polygon with $$$n$$$ vertices such that all the edges and angles are equal.
Now he is shopping: the market has $$$t$$$ regular polygons. For each of them print YES if it is beautiful and NO otherwise.
The first line contains a single integer $$$t$$$ ($$$1 \le t \le 10^4$$$) — the number of polygons in the market.
Each of the next $$$t$$$ lines contains a single integer $$$n_i$$$ ($$$3 \le n_i \le 10^9$$$): it means that the $$$i$$$-th polygon is a regular $$$n_i$$$-sided polygon.
For each polygon, print YES if it's beautiful or NO otherwise (case insensitive).
4 3 4 12 1000000000
NO YES YES YES
In the example, there are $$$4$$$ polygons in the market. It's easy to see that an equilateral triangle (a regular $$$3$$$-sided polygon) is not beautiful, a square (a regular $$$4$$$-sided polygon) is beautiful and a regular $$$12$$$-sided polygon (is shown below) is beautiful as well.
Informação
Provedor Codeforces
Código CF1369A
Tags
Submetido 0
BOUA! 0
Taxa de BOUA's 0%
Datas 09/05/2023 10:03:50
Relacionados