Tree Modification

1000ms

262144K

Description:

You are given a tree with $$$n$$$ vertices. You are allowed to modify the structure of the tree through the following multi-step operation:

Choose three vertices $$$a$$$, $$$b$$$, and $$$c$$$ such that $$$b$$$ is adjacent to both $$$a$$$ and $$$c$$$.
For every vertex $$$d$$$ other than $$$b$$$ that is adjacent to $$$a$$$, remove the edge connecting $$$d$$$ and $$$a$$$ and add the edge connecting $$$d$$$ and $$$c$$$.
Delete the edge connecting $$$a$$$ and $$$b$$$ and add the edge connecting $$$a$$$ and $$$c$$$.

As an example, consider the following tree:

$\text{[math]}$

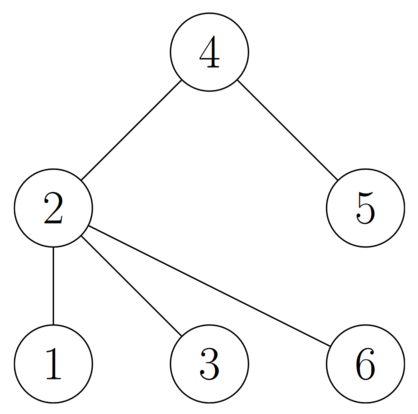
The following diagram illustrates the sequence of steps that happen when we apply an operation to vertices $$$2$$$, $$$4$$$, and $$$5$$$:

$\text{[math]}$

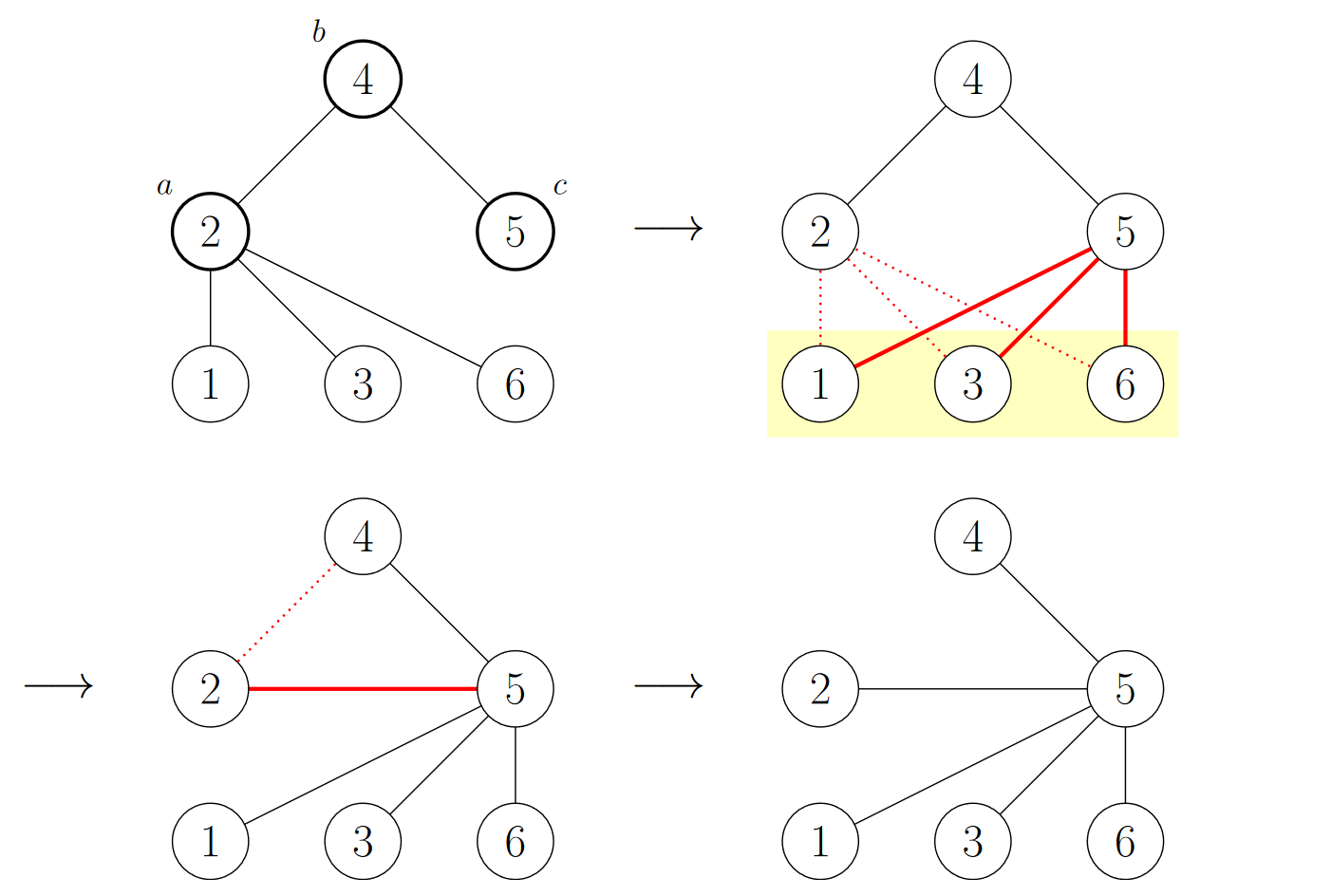
It can be proven that after each operation, the resulting graph is still a tree.

Find the minimum number of operations that must be performed to transform the tree into a star. A star is a tree with one vertex of degree $$$n - 1$$$, called its center, and $$$n - 1$$$ vertices of degree $$$1$$$.

Input:

The first line contains an integer $$$n$$$ ($$$3 \le n \le 2 \cdot 10^5$$$) — the number of vertices in the tree.

The $$$i$$$-th of the following $$$n - 1$$$ lines contains two integers $$$u_i$$$ and $$$v_i$$$ ($$$1 \le u_i, v_i \le n$$$, $$$u_i \neq v_i$$$) denoting that there exists an edge connecting vertices $$$u_i$$$ and $$$v_i$$$. It is guaranteed that the given edges form a tree.

Output:

Print a single integer — the minimum number of operations needed to transform the tree into a star.

It can be proven that under the given constraints, it is always possible to transform the tree into a star using at most $$$10^{18}$$$ operations.

Sample Input:

Sample Output:

Sample Input:

Sample Output:

Note:

The first test case corresponds to the tree shown in the statement. As we have seen before, we can transform the tree into a star with center at vertex $$$5$$$ by applying a single operation to vertices $$$2$$$, $$$4$$$, and $$$5$$$.

In the second test case, the given tree is already a star with the center at vertex $$$4$$$, so no operations have to be performed.

Informação

Provedor Codeforces

Código CF1375G