Special Edges

Description:

Input:

The first line of the input contains four integers $$$n$$$, $$$m$$$, $$$k$$$, $$$q$$$ ($$$2 \le n \le 10^4$$$, $$$1 \le m \le 10^4$$$, $$$1 \le k \le \min(10, m)$$$, $$$1 \le q \le 2 \cdot 10^5$$$) — the number of nodes, the number of edges, the number of special edges and the number of queries.

Each of the next $$$m$$$ lines contains three integers $$$u$$$, $$$v$$$, $$$w$$$ ($$$1 \le u, v \le n$$$; $$$0 \le w \le 25$$$) — the description of a directed edge from node $$$u$$$ to node $$$v$$$ with capacity $$$w$$$.

Edges are numbered starting from $$$1$$$ in the same order they are listed in the input. The first $$$k$$$ edges are the special edges. It is guaranteed that $$$w_i = 0$$$ for all $$$i$$$ with $$$1 \le i \le k$$$.

Each of the next $$$q$$$ lines contains $$$k$$$ integers $$$w_1, w_2, \ldots, w_k$$$ ($$$0 \le w_i \le 25$$$)  — the description of the query. $$$w_i$$$ denotes the capacity of $$$i$$$-th edge.

Output:

For the $$$i$$$-th query, print one integer $$$res_i$$$  — the maximum flow that can be obtained from node $$$1$$$ to node $$$n$$$ given the $$$i$$$-th query's special edge weights.

Sample Input:

2 1 1 3
1 2 0
0
1
2

Sample Output:

0
1
2

Sample Input:

4 4 2 5
1 2 0
2 3 0
2 4 5
3 4 2
0 0
1 10
10 0
7 1
7 2

Sample Output:

0
1
5
6
7

Note:

For the second sample, the following images correspond to the first two queries (from left to right respectively). For each edge there is a pair flow/capacity denoting flow pushed through the edge and edge's capacity. The special edges are colored in red.

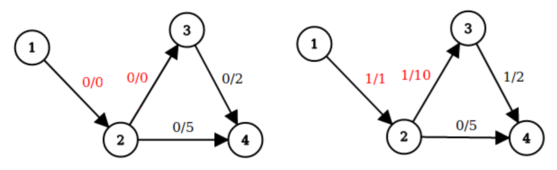
As you can see in first query maximum flow from node $$$1$$$ to node $$$4$$$ equals $$$0$$$ and in second query equals $$$1$$$.