Pairs of Pairs

Description:

Input:

Each test contains multiple test cases. The first line contains the number of test cases $$$t$$$ ($$$1 \le t \le 10^5$$$). Description of the test cases follows.

The first line of each test case contains $$$2$$$ integers $$$n, m$$$ ($$$2 \le n \le 5\cdot 10^5$$$, $$$1 \le m \le 10^6$$$), denoting the number of nodes and edges, respectively.

The next $$$m$$$ lines each contain $$$2$$$ integers $$$u$$$ and $$$v$$$ ($$$1 \le u, v \le n$$$, $$$u \neq v$$$), denoting that there is an undirected edge between nodes $$$u$$$ and $$$v$$$ in the given graph.

It is guaranteed that the given graph is connected, and simple  — it does not contain multiple edges between the same pair of nodes, nor does it have any self-loops.

It is guaranteed that the sum of $$$n$$$ over all test cases does not exceed $$$5\cdot 10^5$$$.

It is guaranteed that the sum of $$$m$$$ over all test cases does not exceed $$$10^6$$$.

Output:

For each test case, the output format is as follows.

If you have found a pairing, in the first line output "PAIRING" (without quotes).

• Then, output $$$k$$$ ($$$\lceil \frac{n}{2} \rceil \le 2\cdot k \le n$$$), the number of pairs in your pairing.
• Then, in each of the next $$$k$$$ lines, output $$$2$$$ integers $$$a$$$ and $$$b$$$  — denoting that $$$a$$$ and $$$b$$$ are paired with each other. Note that the graph does not have to have an edge between $$$a$$$ and $$$b$$$!
• This pairing has to be valid, and every node has to be a part of at most $$$1$$$ pair.

Otherwise, in the first line output "PATH" (without quotes).

• Then, output $$$k$$$ ($$$\lceil \frac{n}{2} \rceil \le k \le n$$$), the number of nodes in your path.
• Then, in the second line, output $$$k$$$ integers, $$$v_1, v_2, \ldots, v_k$$$, in the order in which they appear on the path. Formally, $$$v_i$$$ and $$$v_{i+1}$$$ should have an edge between them for every $$$i$$$ ($$$1 \le i < k$$$).
• This path has to be simple, meaning no node should appear more than once.

Sample Input:

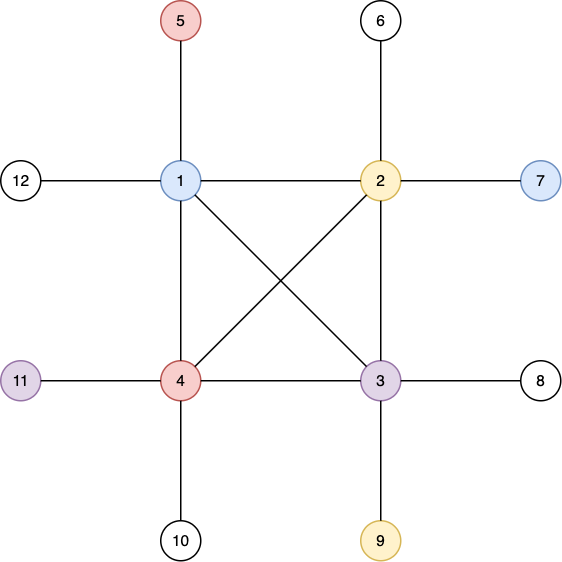
4
6 5
1 4
2 5
3 6
1 5
3 5
6 5
1 4
2 5
3 6
1 5
3 5
12 14
1 2
2 3
3 4
4 1
1 5
1 12
2 6
2 7
3 8
3 9
4 10
4 11
2 4
1 3
12 14
1 2
2 3
3 4
4 1
1 5
1 12
2 6
2 7
3 8
3 9
4 10
4 11
2 4
1 3

Sample Output:

PATH
4 
1 5 3 6
PAIRING
2
1 6
2 4
PAIRING
3
1 8
2 5
4 10
PAIRING
4
1 7
2 9
3 11
4 5

Note:

The path outputted in the first case is the following.

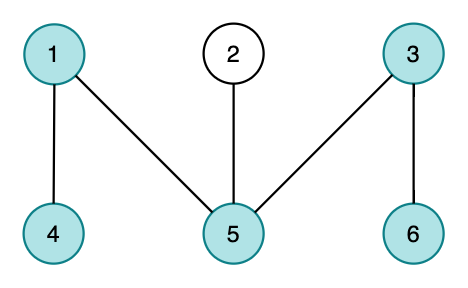
The pairing outputted in the second case is the following.

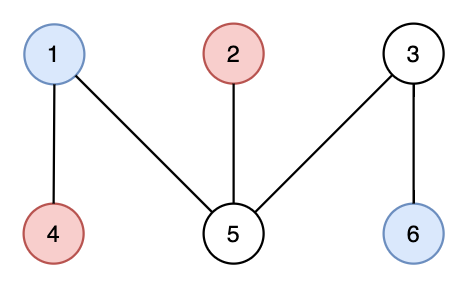
Here is an invalid pairing for the same graph  — the subgraph $$$\{1,3,4,5\}$$$ has $$$3$$$ edges.

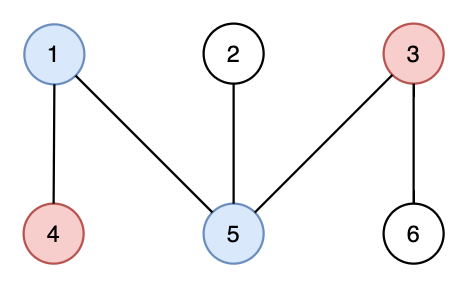
Here is the pairing outputted in the third case.

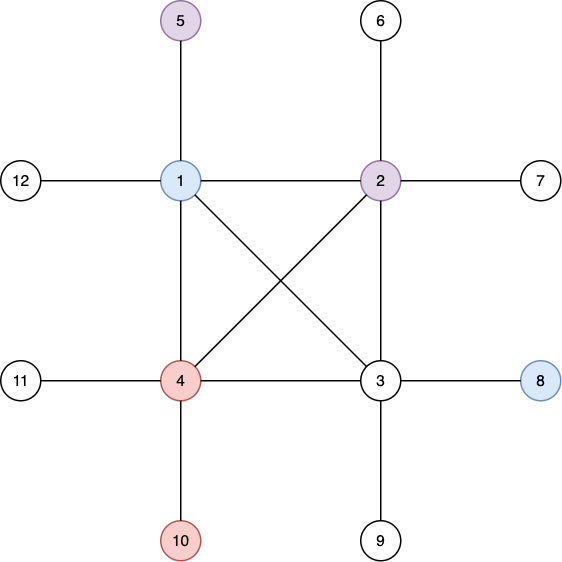
It's valid because —

• The subgraph $$$\{1,8,2,5\}$$$ has edges ($$$1$$$,$$$2$$$) and ($$$1$$$,$$$5$$$).
• The subgraph $$$\{1,8,4,10\}$$$ has edges ($$$1$$$,$$$4$$$) and ($$$4$$$,$$$10$$$).
• The subgraph $$$\{4,10,2,5\}$$$ has edges ($$$2$$$,$$$4$$$) and ($$$4$$$,$$$10$$$).

Here is the pairing outputted in the fourth case.