Preparando MOJI
One evening Rainbow Dash and Fluttershy have come up with a game. Since the ponies are friends, they have decided not to compete in the game but to pursue a common goal.
The game starts on a square flat grid, which initially has the outline borders built up. Rainbow Dash and Fluttershy have flat square blocks with size $$$1\times1$$$, Rainbow Dash has an infinite amount of light blue blocks, Fluttershy has an infinite amount of yellow blocks.
The blocks are placed according to the following rule: each newly placed block must touch the built on the previous turns figure by a side (note that the outline borders of the grid are built initially). At each turn, one pony can place any number of blocks of her color according to the game rules.
Rainbow and Fluttershy have found out that they can build patterns on the grid of the game that way. They have decided to start with something simple, so they made up their mind to place the blocks to form a chess coloring. Rainbow Dash is well-known for her speed, so she is interested in the minimum number of turns she and Fluttershy need to do to get a chess coloring, covering the whole grid with blocks. Please help her find that number!
Since the ponies can play many times on different boards, Rainbow Dash asks you to find the minimum numbers of turns for several grids of the games.
The chess coloring in two colors is the one in which each square is neighbor by side only with squares of different colors.
The first line contains a single integer $$$T$$$ ($$$1 \le T \le 100$$$): the number of grids of the games.
Each of the next $$$T$$$ lines contains a single integer $$$n$$$ ($$$1 \le n \le 10^9$$$): the size of the side of the grid of the game.
For each grid of the game print the minimum number of turns required to build a chess coloring pattern out of blocks on it.
2 3 4
2 3
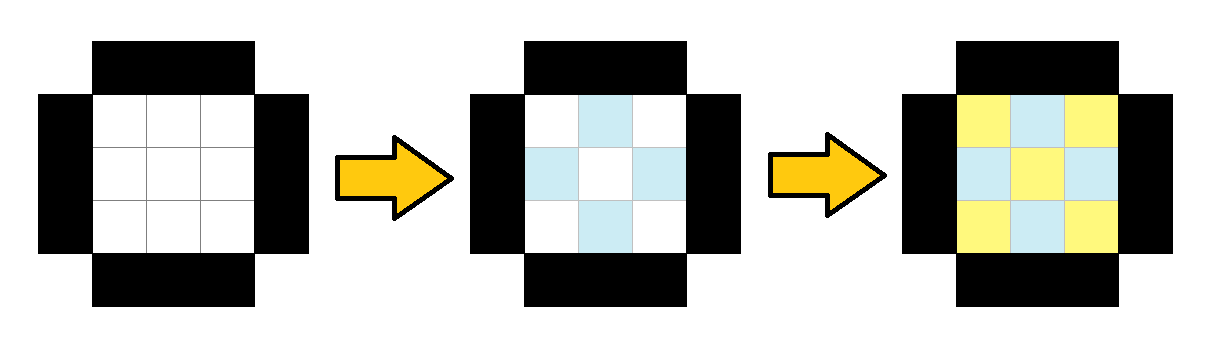
For $$$3\times3$$$ grid ponies can make two following moves: