Boboniu and Jianghu

1000ms

262144K

Description:

Since Boboniu finished building his Jianghu, he has been doing Kungfu on these mountains every day.

Boboniu designs a map for his $$$n$$$ mountains. He uses $$$n-1$$$ roads to connect all $$$n$$$ mountains. Every pair of mountains is connected via roads.

For the $$$i$$$-th mountain, Boboniu estimated the tiredness of doing Kungfu on the top of it as $$$t_i$$$. He also estimated the height of each mountain as $$$h_i$$$.

A path is a sequence of mountains $$$M$$$ such that for each $$$i$$$ ($$$1 \le i < |M|$$$), there exists a road between $$$M_i$$$ and $$$M_{i+1}$$$. Boboniu would regard the path as a challenge if for each $$$i$$$ ($$$1\le i<|M|$$$), $$$h_{M_i}\le h_{M_{i+1}}$$$.

Boboniu wants to divide all $$$n-1$$$ roads into several challenges. Note that each road must appear in exactly one challenge, but a mountain may appear in several challenges.

Boboniu wants to minimize the total tiredness to do all the challenges. The tiredness of a challenge $$$M$$$ is the sum of tiredness of all mountains in it, i.e. $$$\sum_{i=1}^{|M|}t_{M_i}$$$.

He asked you to find the minimum total tiredness. As a reward for your work, you'll become a guardian in his Jianghu.

Input:

The first line contains a single integer $$$n$$$ ($$$2 \le n \le 2 \cdot 10^5$$$), denoting the number of the mountains.

The second line contains $$$n$$$ integers $$$t_1, t_2, \ldots, t_n$$$ ($$$1 \le t_i \le 10^6$$$), denoting the tiredness for Boboniu to do Kungfu on each mountain.

The third line contains $$$n$$$ integers $$$h_1, h_2, \ldots, h_n$$$ ($$$1 \le h_i \le 10^6$$$), denoting the height of each mountain.

Each of the following $$$n - 1$$$ lines contains two integers $$$u_i$$$, $$$v_i$$$ ($$$1 \le u_i, v_i \le n, u_i \neq v_i$$$), denoting the ends of the road. It's guaranteed that all mountains are connected via roads.

Output:

Print one integer: the smallest sum of tiredness of all challenges.

Sample Input:

5
40 10 30 50 20
2 3 2 3 1
1 2
1 3
2 4
2 5

Sample Output:

Sample Input:

5
1000000 1 1 1 1
1000000 1 1 1 1
1 2
1 3
1 4
1 5

Sample Output:

Sample Input:

10
510916 760492 684704 32545 484888 933975 116895 77095 127679 989957
402815 705067 705067 705067 623759 103335 749243 138306 138306 844737
1 2
3 2
4 3
1 5
6 4
6 7
8 7
8 9
9 10

Sample Output:

Note:

For the first example:

$\text{[math]}$

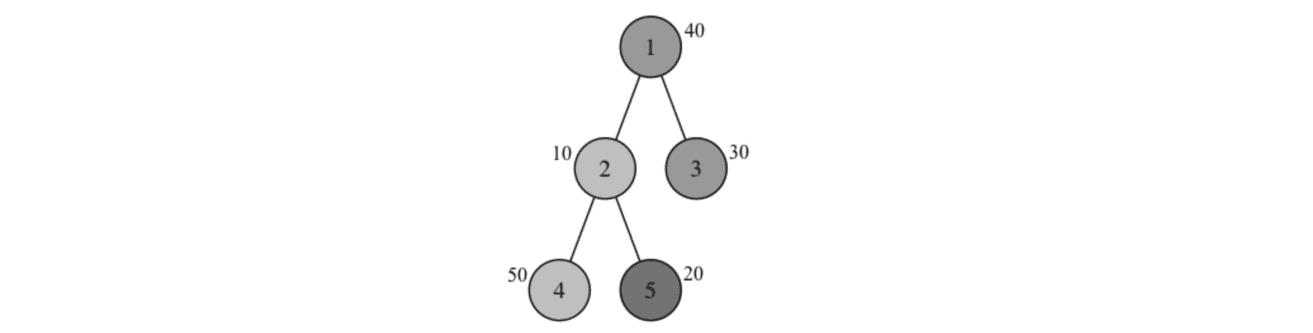
In the picture, the lighter a point is, the higher the mountain it represents. One of the best divisions is:

Challenge $$$1$$$: $$$3 \to 1 \to 2$$$
Challenge $$$2$$$: $$$5 \to 2 \to 4$$$

The total tiredness of Boboniu is $$$(30 + 40 + 10) + (20 + 10 + 50) = 160$$$. It can be shown that this is the minimum total tiredness.

Informação

Provedor Codeforces

Código CF1394D