Preparando MOJI
Boboniu likes playing chess with his employees. As we know, no employee can beat the boss in the chess game, so Boboniu has never lost in any round.
You are a new applicant for his company. Boboniu will test you with the following chess question:
Consider a $$$n\times m$$$ grid (rows are numbered from $$$1$$$ to $$$n$$$, and columns are numbered from $$$1$$$ to $$$m$$$). You have a chess piece, and it stands at some cell $$$(S_x,S_y)$$$ which is not on the border (i.e. $$$2 \le S_x \le n-1$$$ and $$$2 \le S_y \le m-1$$$).
From the cell $$$(x,y)$$$, you can move your chess piece to $$$(x,y')$$$ ($$$1\le y'\le m, y' \neq y$$$) or $$$(x',y)$$$ ($$$1\le x'\le n, x'\neq x$$$). In other words, the chess piece moves as a rook. From the cell, you can move to any cell on the same row or column.
Your goal is to visit each cell exactly once. Can you find a solution?
Note that cells on the path between two adjacent cells in your route are not counted as visited, and it is not required to return to the starting point.
The only line of the input contains four integers $$$n$$$, $$$m$$$, $$$S_x$$$ and $$$S_y$$$ ($$$3\le n,m\le 100$$$, $$$2 \le S_x \le n-1$$$, $$$2 \le S_y \le m-1$$$) — the number of rows, the number of columns, and the initial position of your chess piece, respectively.
You should print $$$n\cdot m$$$ lines.
The $$$i$$$-th line should contain two integers $$$x_i$$$ and $$$y_i$$$ ($$$1 \leq x_i \leq n$$$, $$$1 \leq y_i \leq m$$$), denoting the $$$i$$$-th cell that you visited. You should print exactly $$$nm$$$ pairs $$$(x_i, y_i)$$$, they should cover all possible pairs $$$(x_i, y_i)$$$, such that $$$1 \leq x_i \leq n$$$, $$$1 \leq y_i \leq m$$$.
We can show that under these constraints there always exists a solution. If there are multiple answers, print any.
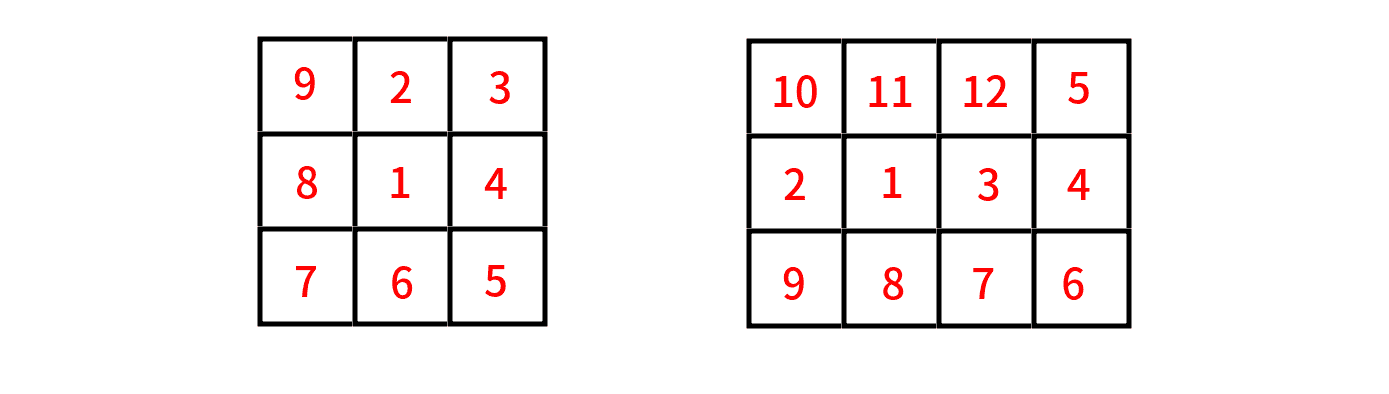
3 3 2 2
2 2 1 2 1 3 2 3 3 3 3 2 3 1 2 1 1 1
3 4 2 2
2 2 2 1 2 3 2 4 1 4 3 4 3 3 3 2 3 1 1 1 1 2 1 3
Possible routes for two examples: