Maximum Distributed Tree

Description:

Input:

The first line contains one integer $$$t$$$ ($$$1 \le t \le 100$$$) — the number of test cases.

The first line of each test case contains a single integer $$$n$$$ ($$$2 \le n \le 10^5$$$) — the number of nodes in the tree.

Each of the next $$$n-1$$$ lines describes an edge: the $$$i$$$-th line contains two integers $$$u_i$$$ and $$$v_i$$$ ($$$1 \le u_i, v_i \le n$$$; $$$u_i \ne v_i$$$) — indices of vertices connected by the $$$i$$$-th edge.

Next line contains a single integer $$$m$$$ ($$$1 \le m \le 6 \cdot 10^4$$$) — the number of prime factors of $$$k$$$.

Next line contains $$$m$$$ prime numbers $$$p_1, p_2, \ldots, p_m$$$ ($$$2 \le p_i < 6 \cdot 10^4$$$) such that $$$k = p_1 \cdot p_2 \cdot \ldots \cdot p_m$$$.

It is guaranteed that the sum of $$$n$$$ over all test cases doesn't exceed $$$10^5$$$, the sum of $$$m$$$ over all test cases doesn't exceed $$$6 \cdot 10^4$$$, and the given edges for each test cases form a tree.

Output:

Print the maximum distribution index you can get. Since answer can be too large, print it modulo $$$10^9+7$$$.

Sample Input:

3
4
1 2
2 3
3 4
2
2 2
4
3 4
1 3
3 2
2
3 2
7
6 1
2 3
4 6
7 3
5 1
3 6
4
7 5 13 3

Sample Output:

17
18
286

Note:

In the first test case, one of the optimal ways is on the following image:

In this case, $$$f(1,2)=1$$$, $$$f(1,3)=3$$$, $$$f(1,4)=5$$$, $$$f(2,3)=2$$$, $$$f(2,4)=4$$$, $$$f(3,4)=2$$$, so the sum of these $$$6$$$ numbers is $$$17$$$.

In the second test case, one of the optimal ways is on the following image:

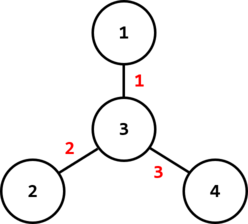
In this case, $$$f(1,2)=3$$$, $$$f(1,3)=1$$$, $$$f(1,4)=4$$$, $$$f(2,3)=2$$$, $$$f(2,4)=5$$$, $$$f(3,4)=3$$$, so the sum of these $$$6$$$ numbers is $$$18$$$.