Tree Tag

1000ms

262144K

Description:

Alice and Bob are playing a fun game of tree tag.

The game is played on a tree of $$$n$$$ vertices numbered from $$$1$$$ to $$$n$$$. Recall that a tree on $$$n$$$ vertices is an undirected, connected graph with $$$n-1$$$ edges.

Initially, Alice is located at vertex $$$a$$$, and Bob at vertex $$$b$$$. They take turns alternately, and Alice makes the first move. In a move, Alice can jump to a vertex with distance at most $$$da$$$ from the current vertex. And in a move, Bob can jump to a vertex with distance at most $$$db$$$ from the current vertex. The distance between two vertices is defined as the number of edges on the unique simple path between them. In particular, either player is allowed to stay at the same vertex in a move. Note that when performing a move, a player only occupies the starting and ending vertices of their move, not the vertices between them.

If after at most $$$10^{100}$$$ moves, Alice and Bob occupy the same vertex, then Alice is declared the winner. Otherwise, Bob wins.

Determine the winner if both players play optimally.

Input:

Each test contains multiple test cases. The first line contains the number of test cases $$$t$$$ ($$$1 \le t \le 10^4$$$). Description of the test cases follows.

The first line of each test case contains five integers $$$n,a,b,da,db$$$ ($$$2\le n\le 10^5$$$, $$$1\le a,b\le n$$$, $$$a\ne b$$$, $$$1\le da,db\le n-1$$$) — the number of vertices, Alice's vertex, Bob's vertex, Alice's maximum jumping distance, and Bob's maximum jumping distance, respectively.

The following $$$n-1$$$ lines describe the edges of the tree. The $$$i$$$-th of these lines contains two integers $$$u$$$, $$$v$$$ ($$$1\le u, v\le n, u\ne v$$$), denoting an edge between vertices $$$u$$$ and $$$v$$$. It is guaranteed that these edges form a tree structure.

It is guaranteed that the sum of $$$n$$$ across all test cases does not exceed $$$10^5$$$.

Output:

For each test case, output a single line containing the winner of the game: "Alice" or "Bob".

Sample Input:

4
4 3 2 1 2
1 2
1 3
1 4
6 6 1 2 5
1 2
6 5
2 3
3 4
4 5
9 3 9 2 5
1 2
1 6
1 9
1 3
9 5
7 9
4 8
4 3
11 8 11 3 3
1 2
11 9
4 9
6 5
2 10
3 2
5 9
8 3
7 4
7 10

Sample Output:

Alice
Bob
Alice
Alice

Note:

In the first test case, Alice can win by moving to vertex $$$1$$$. Then wherever Bob moves next, Alice will be able to move to the same vertex on the next move.

$\text{[math]}$

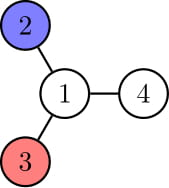
In the second test case, Bob has the following strategy to win. Wherever Alice moves, Bob will always move to whichever of the two vertices $$$1$$$ or $$$6$$$ is farthest from Alice.

$\text{[math]}$

Informação

Provedor Codeforces

Código CF1404B