Errich-Tac-Toe (Hard Version)

1000ms

262144K

Description:

The only difference between the easy and hard versions is that tokens of type O do not appear in the input of the easy version.

Errichto gave Monogon the following challenge in order to intimidate him from taking his top contributor spot on Codeforces.

In a Tic-Tac-Toe grid, there are $$$n$$$ rows and $$$n$$$ columns. Each cell of the grid is either empty or contains a token. There are two types of tokens: X and O. If there exist three tokens of the same type consecutive in a row or column, it is a winning configuration. Otherwise, it is a draw configuration.

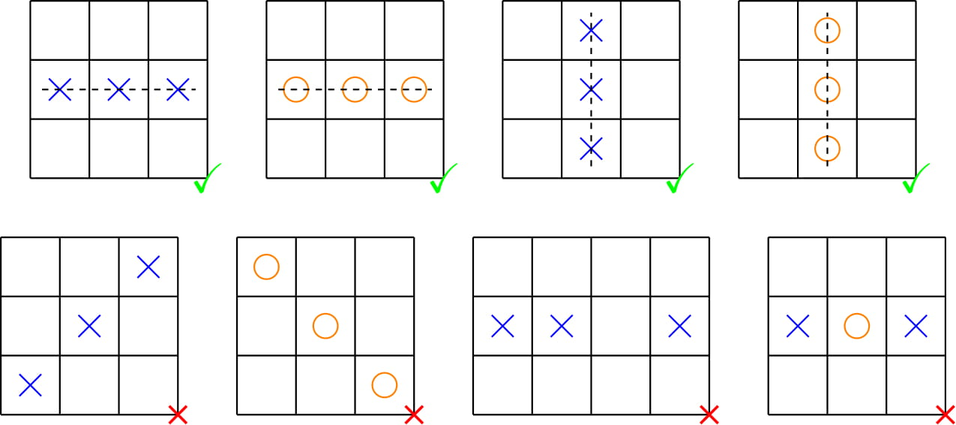$\text{[math]}$ The patterns in the first row are winning configurations. The patterns in the second row are draw configurations.

In an operation, you can change an X to an O, or an O to an X. Let $$$k$$$ denote the total number of tokens in the grid. Your task is to make the grid a draw in at most $$$\lfloor \frac{k}{3}\rfloor$$$ (rounding down) operations.

You are not required to minimize the number of operations.

Input:

The first line contains a single integer $$$t$$$ ($$$1\le t\le 100$$$) — the number of test cases.

The first line of each test case contains a single integer $$$n$$$ ($$$1\le n\le 300$$$) — the size of the grid.

The following $$$n$$$ lines each contain a string of $$$n$$$ characters, denoting the initial grid. The character in the $$$i$$$-th row and $$$j$$$-th column is '.' if the cell is empty, or it is the type of token in the cell: 'X' or 'O'.

It is guaranteed that not all cells are empty.

The sum of $$$n$$$ across all test cases does not exceed $$$300$$$.

Output:

For each test case, print the state of the grid after applying the operations.

We have proof that a solution always exists. If there are multiple solutions, print any.

Sample Input:

3
3
.O.
OOO
.O.
6
XXXOOO
XXXOOO
XX..OO
OO..XX
OOOXXX
OOOXXX
5
.OOO.
OXXXO
OXXXO
OXXXO
.OOO.

Sample Output:

.O.
OXO
.O.
OXXOOX
XOXOXO
XX..OO
OO..XX
OXOXOX
XOOXXO
.OXO.
OOXXO
XXOXX
OXXOO
.OXO.

Note:

In the first test case, there are initially three 'O' consecutive in the second row and the second column. By changing the middle token to 'X' we make the grid a draw, and we only changed $$$1\le \lfloor 5/3\rfloor$$$ token.

In the second test case, the final grid is a draw. We only changed $$$8\le \lfloor 32/3\rfloor$$$ tokens.

In the third test case, the final grid is a draw. We only changed $$$7\le \lfloor 21/3\rfloor$$$ tokens.

Informação

Provedor Codeforces

Código CF1450C2