Dog Snacks

Description:

Input:

Each test contains one or more test cases. The first line contains the number of test cases $$$t$$$ ($$$1 \le t \le 10^4$$$).

The first line of each test case contains one integer $$$n$$$ ($$$2 \le n \le 2 \cdot 10^5$$$) — the number of intersections of the park.

The next $$$n-1$$$ lines contain two integers $$$u$$$ and $$$v$$$ ($$$1 \le u,v \le n$$$, $$$u \ne v$$$) each, which means there is a road between intersection $$$u$$$ and $$$v$$$. All roads are bidirectional and distinct.

It is guaranteed that:

• For each test case, for every $$$a$$$ and $$$b$$$ ($$$1 \le a, b \le n$$$), it is possible to get to the $$$b$$$-th intersection from the $$$a$$$-th intersection.
• The sum of $$$n$$$ in all test cases doesn't exceed $$$2 \cdot 10^5$$$.

Output:

For each test case, print one integer — the minimum possible value of $$$k$$$ such that Badugi can complete the mission.

Sample Input:

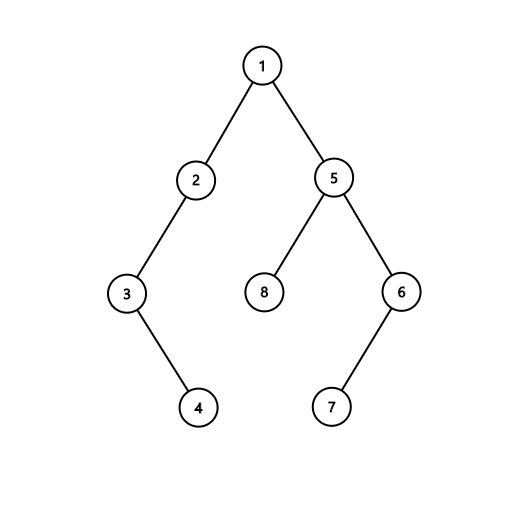
3
3
1 2
1 3
4
1 2
2 3
3 4
8
1 2
2 3
3 4
1 5
5 6
6 7
5 8

Sample Output:

2
3
3

Note:

In the first case, Badugi can complete his mission with $$$k=2$$$ by moving as follows:

1. Initially, Badugi is at the $$$1$$$-st intersection. The closest snack is obviously at the $$$1$$$-st intersection, so he just eats it.
2. Next, he looks for the closest snack, which can be either the one at the $$$2$$$-nd or the one at the $$$3$$$-rd intersection. Assume that he chooses the $$$2$$$-nd intersection. He moves to the $$$2$$$-nd intersection, which is $$$1$$$ meter away, and eats the snack.
3. Now the only remaining snack is on the $$$3$$$-rd intersection, and he needs to move along $$$2$$$ paths to get to it.
4. After eating the snack at the $$$3$$$-rd intersection, he needs to find the $$$1$$$-st intersection again, which is only $$$1$$$ meter away. As he gets back to it, he completes the mission.

In the second case, the only possible sequence of moves he can make is $$$1$$$ – $$$2$$$ – $$$3$$$ – $$$4$$$ – $$$1$$$. Since the distance between the $$$4$$$-th intersection and the $$$1$$$-st intersection is $$$3$$$, $$$k$$$ needs to be at least $$$3$$$ for Badugi to complete his mission.

In the third case, Badugi can make his moves as follows: $$$1$$$ – $$$5$$$ – $$$6$$$ – $$$7$$$ – $$$8$$$ – $$$2$$$ – $$$3$$$ – $$$4$$$ – $$$1$$$. It can be shown that this is the only possible sequence of moves for Badugi to complete his mission with $$$k=3$$$.