Preparando MOJI
You have $$$n$$$ chains, the $$$i$$$-th chain consists of $$$c_i$$$ vertices. Vertices in each chain are numbered independently from $$$1$$$ to $$$c_i$$$ along the chain. In other words, the $$$i$$$-th chain is the undirected graph with $$$c_i$$$ vertices and $$$(c_i - 1)$$$ edges connecting the $$$j$$$-th and the $$$(j + 1)$$$-th vertices for each $$$1 \le j < c_i$$$.
Now you decided to unite chains in one graph in the following way:
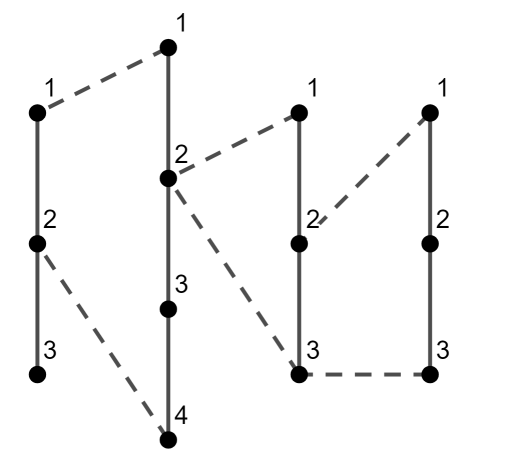 Picture of the first test case. Dotted lines are the edges added during uniting process
Picture of the first test case. Dotted lines are the edges added during uniting process Calculate the length of the longest simple cycle in the resulting graph.
A simple cycle is a chain where the first and last vertices are connected as well. If you travel along the simple cycle, each vertex of this cycle will be visited exactly once.
The first line contains a single integer $$$t$$$ ($$$1 \le t \le 1000$$$) — the number of test cases.
The first line of each test case contains the single integer $$$n$$$ ($$$2 \le n \le 10^5$$$) — the number of chains you have.
The second line of each test case contains $$$n$$$ integers $$$c_1, c_2, \dots, c_n$$$ ($$$2 \le c_i \le 10^9$$$) — the number of vertices in the corresponding chains.
The third line of each test case contains $$$n$$$ integers $$$a_1, a_2, \dots, a_n$$$ ($$$a_1 = -1$$$; $$$1 \le a_i \le c_{i - 1}$$$).
The fourth line of each test case contains $$$n$$$ integers $$$b_1, b_2, \dots, b_n$$$ ($$$b_1 = -1$$$; $$$1 \le b_i \le c_{i - 1}$$$).
Both $$$a_1$$$ and $$$b_1$$$ are equal to $$$-1$$$, they aren't used in graph building and given just for index consistency. It's guaranteed that the sum of $$$n$$$ over all test cases doesn't exceed $$$10^5$$$.
For each test case, print the length of the longest simple cycle.
3 4 3 4 3 3 -1 1 2 2 -1 2 2 3 2 5 6 -1 5 -1 1 3 3 5 2 -1 1 1 -1 3 5
7 11 8
In the first test case, the longest simple cycle is shown below:
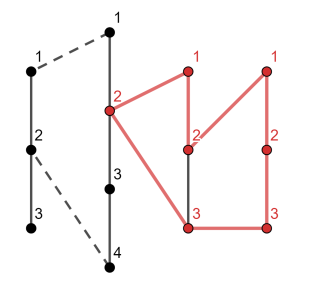
We can't increase it with the first chain, since in such case it won't be simple — the vertex $$$2$$$ on the second chain will break simplicity.