Move and Swap

2000ms

262144K

Description:

You are given $$$n - 1$$$ integers $$$a_2, \dots, a_n$$$ and a tree with $$$n$$$ vertices rooted at vertex $$$1$$$. The leaves are all at the same distance $$$d$$$ from the root.

Recall that a tree is a connected undirected graph without cycles. The distance between two vertices is the number of edges on the simple path between them. All non-root vertices with degree $$$1$$$ are leaves. If vertices $$$s$$$ and $$$f$$$ are connected by an edge and the distance of $$$f$$$ from the root is greater than the distance of $$$s$$$ from the root, then $$$f$$$ is called a child of $$$s$$$.

Initially, there are a red coin and a blue coin on the vertex $$$1$$$. Let $$$r$$$ be the vertex where the red coin is and let $$$b$$$ be the vertex where the blue coin is. You should make $$$d$$$ moves. A move consists of three steps:

Move the red coin to any child of $$$r$$$.
Move the blue coin to any vertex $$$b'$$$ such that $$$dist(1, b') = dist(1, b) + 1$$$. Here $$$dist(x, y)$$$ indicates the length of the simple path between $$$x$$$ and $$$y$$$. Note that $$$b$$$ and $$$b'$$$ are not necessarily connected by an edge.
You can optionally swap the two coins (or skip this step).

Note that $$$r$$$ and $$$b$$$ can be equal at any time, and there is no number written on the root.

After each move, you gain $$$|a_r - a_b|$$$ points. What's the maximum number of points you can gain after $$$d$$$ moves?

Input:

The first line contains a single integer $$$t$$$ ($$$1 \le t \le 10^4$$$) — the number of test cases.

The first line of each test case contains a single integer $$$n$$$ ($$$2 \leq n \leq 2 \cdot 10^5$$$) — the number of vertices in the tree.

The second line of each test case contains $$$n-1$$$ integers $$$v_2, v_3, \dots, v_n$$$ ($$$1 \leq v_i \leq n$$$, $$$v_i \neq i$$$) — the $$$i$$$-th of them indicates that there is an edge between vertices $$$i$$$ and $$$v_i$$$. It is guaranteed, that these edges form a tree.

The third line of each test case contains $$$n-1$$$ integers $$$a_2, \dots, a_n$$$ ($$$1 \leq a_i \leq 10^9$$$) — the numbers written on the vertices.

It is guaranteed that the sum of $$$n$$$ for all test cases does not exceed $$$2 \cdot 10^5$$$.

Output:

For each test case, print a single integer: the maximum number of points you can gain after $$$d$$$ moves.

Sample Input:

4
14
1 1 1 2 3 4 4 5 5 6 7 8 8
2 3 7 7 6 9 5 9 7 3 6 6 5
6
1 2 2 3 4
32 78 69 5 41
15
1 15 1 10 4 9 11 2 4 1 8 6 10 11
62 13 12 43 39 65 42 86 25 38 19 19 43 62
15
11 2 7 6 9 8 10 1 1 1 5 3 15 2
50 19 30 35 9 45 13 24 8 44 16 26 10 40

Sample Output:

Note:

In the first test case, an optimal solution is to:

move $$$1$$$: $$$r = 4$$$, $$$b = 2$$$; no swap;
move $$$2$$$: $$$r = 7$$$, $$$b = 6$$$; swap (after it $$$r = 6$$$, $$$b = 7$$$);
move $$$3$$$: $$$r = 11$$$, $$$b = 9$$$; no swap.

The total number of points is $$$|7 - 2| + |6 - 9| + |3 - 9| = 14$$$.

$\text{[math]}$

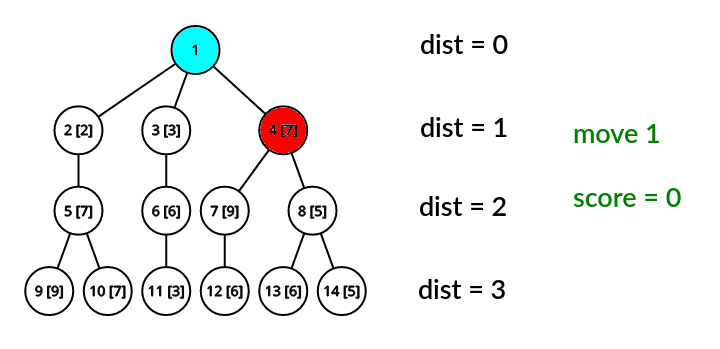
In the second test case, an optimal solution is to:

move $$$1$$$: $$$r = 2$$$, $$$b = 2$$$; no swap;
move $$$2$$$: $$$r = 3$$$, $$$b = 4$$$; no swap;
move $$$3$$$: $$$r = 5$$$, $$$b = 6$$$; no swap.

The total number of points is $$$|32 - 32| + |78 - 69| + |5 - 41| = 45$$$.

Informação

Provedor Codeforces

Código CF1485E