Squares

2000ms

262144K

Description:

There are $$$n$$$ squares drawn from left to right on the floor. The $$$i$$$-th square has three integers $$$p_i,a_i,b_i$$$, written on it. The sequence $$$p_1,p_2,\dots,p_n$$$ forms a permutation.

Each round you will start from the leftmost square $$$1$$$ and jump to the right. If you are now on the $$$i$$$-th square, you can do one of the following two operations:

Jump to the $$$i+1$$$-th square and pay the cost $$$a_i$$$. If $$$i=n$$$, then you can end the round and pay the cost $$$a_i$$$.
Jump to the $$$j$$$-th square and pay the cost $$$b_i$$$, where $$$j$$$ is the leftmost square that satisfies $$$j > i, p_j > p_i$$$. If there is no such $$$j$$$ then you can end the round and pay the cost $$$b_i$$$.

There are $$$q$$$ rounds in the game. To make the game more difficult, you need to maintain a square set $$$S$$$ (initially it is empty). You must pass through these squares during the round (other squares can also be passed through). The square set $$$S$$$ for the $$$i$$$-th round is obtained by adding or removing a square from the square set for the $$$(i-1)$$$-th round.

For each round find the minimum cost you should pay to end it.

Input:

The first line contains two integers $$$n$$$, $$$q$$$ ($$$1\le n,q\le 2 \cdot 10^5$$$) — the number of squares and the number of rounds.

The second line contains $$$n$$$ distinct integers $$$p_1,p_2,\dots,p_n$$$ ($$$1\le p_i\le n$$$). It is guaranteed that the sequence $$$p_1,p_2,\dots,p_n$$$ forms a permutation.

The third line contains $$$n$$$ integers $$$a_1,a_2,\ldots,a_n$$$ ($$$-10^9\le a_i\le 10^9$$$).

The fourth line contains $$$n$$$ integers $$$b_1,b_2,\dots,b_n$$$ ($$$-10^9\le b_i\le 10^9$$$).

Then $$$q$$$ lines follow, $$$i$$$-th of them contains a single integer $$$x_i$$$ ($$$1\le x_i\le n$$$). If $$$x_i$$$ was in the set $$$S$$$ on the $$$(i-1)$$$-th round you should remove it, otherwise, you should add it.

Output:

Print $$$q$$$ lines, each of them should contain a single integer — the minimum cost you should pay to end the corresponding round.

Sample Input:

Sample Output:

6
8

Sample Input:

5 4
2 1 5 3 4
6 -5 3 -10 -1
0 3 2 7 2
1
2
3
2

Sample Output:

-8
-7
-7
-8

Note:

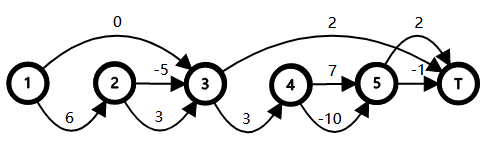
Let's consider the character $$$T$$$ as the end of a round. Then we can draw two graphs for the first and the second test.

$\text{[math]}$ $\text{[math]}$

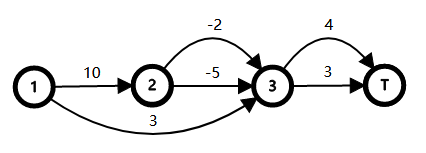
In the first round of the first test, the set that you must pass through is $$$\{1\}$$$. The path you can use is $$$1\to 3\to T$$$ and its cost is $$$6$$$.

In the second round of the first test, the set that you must pass through is $$$\{1,2\}$$$. The path you can use is $$$1\to 2\to 3\to T$$$ and its cost is $$$8$$$.

Informação

Provedor Codeforces

Código CF1495F