Triangular Paths

2000ms

262144K

Description:

Consider an infinite triangle made up of layers. Let's number the layers, starting from one, from the top of the triangle (from top to bottom). The $$$k$$$-th layer of the triangle contains $$$k$$$ points, numbered from left to right. Each point of an infinite triangle is described by a pair of numbers $$$(r, c)$$$ ($$$1 \le c \le r$$$), where $$$r$$$ is the number of the layer, and $$$c$$$ is the number of the point in the layer. From each point $$$(r, c)$$$ there are two directed edges to the points $$$(r+1, c)$$$ and $$$(r+1, c+1)$$$, but only one of the edges is activated. If $$$r + c$$$ is even, then the edge to the point $$$(r+1, c)$$$ is activated, otherwise the edge to the point $$$(r+1, c+1)$$$ is activated. Look at the picture for a better understanding.

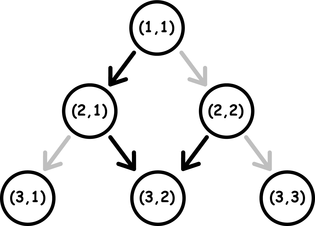$\text{[math]}$ Activated edges are colored in black. Non-activated edges are colored in gray.

From the point $$$(r_1, c_1)$$$ it is possible to reach the point $$$(r_2, c_2)$$$, if there is a path between them only from activated edges. For example, in the picture above, there is a path from $$$(1, 1)$$$ to $$$(3, 2)$$$, but there is no path from $$$(2, 1)$$$ to $$$(1, 1)$$$.

Initially, you are at the point $$$(1, 1)$$$. For each turn, you can:

Replace activated edge for point $$$(r, c)$$$. That is if the edge to the point $$$(r+1, c)$$$ is activated, then instead of it, the edge to the point $$$(r+1, c+1)$$$ becomes activated, otherwise if the edge to the point $$$(r+1, c+1)$$$, then instead if it, the edge to the point $$$(r+1, c)$$$ becomes activated. This action increases the cost of the path by $$$1$$$;
Move from the current point to another by following the activated edge. This action does not increase the cost of the path.

You are given a sequence of $$$n$$$ points of an infinite triangle $$$(r_1, c_1), (r_2, c_2), \ldots, (r_n, c_n)$$$. Find the minimum cost path from $$$(1, 1)$$$, passing through all $$$n$$$ points in arbitrary order.

Input:

The first line contains one integer $$$t$$$ ($$$1 \le t \le 10^4$$$) is the number of test cases. Then $$$t$$$ test cases follow.

Each test case begins with a line containing one integer $$$n$$$ ($$$1 \le n \le 2 \cdot 10^5$$$) is the number of points to visit.

The second line contains $$$n$$$ numbers $$$r_1, r_2, \ldots, r_n$$$ ($$$1 \le r_i \le 10^9$$$), where $$$r_i$$$ is the number of the layer in which $$$i$$$-th point is located.

The third line contains $$$n$$$ numbers $$$c_1, c_2, \ldots, c_n$$$ ($$$1 \le c_i \le r_i$$$), where $$$c_i$$$ is the number of the $$$i$$$-th point in the $$$r_i$$$ layer.

It is guaranteed that all $$$n$$$ points are distinct.

It is guaranteed that there is always at least one way to traverse all $$$n$$$ points.

It is guaranteed that the sum of $$$n$$$ over all test cases does not exceed $$$2 \cdot 10^5$$$.

Output:

For each test case, output the minimum cost of a path passing through all points in the corresponding test case.

Sample Input:

4
3
1 4 2
1 3 1
2
2 4
2 3
2
1 1000000000
1 1000000000
4
3 10 5 8
2 5 2 4

Sample Output:

Informação

Provedor Codeforces

Código CF1506F