Optimal Encoding

7000ms

1048576K

Description:

Touko's favorite sequence of numbers is a permutation $$$a_1, a_2, \dots, a_n$$$ of $$$1, 2, \dots, n$$$, and she wants some collection of permutations that are similar to her favorite permutation.

She has a collection of $$$q$$$ intervals of the form $$$[l_i, r_i]$$$ with $$$1 \le l_i \le r_i \le n$$$. To create permutations that are similar to her favorite permutation, she coined the following definition:

A permutation $$$b_1, b_2, \dots, b_n$$$ allows an interval $$$[l', r']$$$ to holds its shape if for any pair of integers $$$(x, y)$$$ such that $$$l' \le x < y \le r'$$$, we have $$$b_x < b_y$$$ if and only if $$$a_x < a_y$$$.
A permutation $$$b_1, b_2, \dots, b_n$$$ is $$$k$$$-similar if $$$b$$$ allows all intervals $$$[l_i, r_i]$$$ for all $$$1 \le i \le k$$$ to hold their shapes.

Yuu wants to figure out all $$$k$$$-similar permutations for Touko, but it turns out this is a very hard task; instead, Yuu will encode the set of all $$$k$$$-similar permutations with directed acylic graphs (DAG). Yuu also coined the following definitions for herself:

A permutation $$$b_1, b_2, \dots, b_n$$$ satisfies a DAG $$$G'$$$ if for all edge $$$u \to v$$$ in $$$G'$$$, we must have $$$b_u < b_v$$$.
A $$$k$$$-encoding is a DAG $$$G_k$$$ on the set of vertices $$$1, 2, \dots, n$$$ such that a permutation $$$b_1, b_2, \dots, b_n$$$ satisfies $$$G_k$$$ if and only if $$$b$$$ is $$$k$$$-similar.

Since Yuu is free today, she wants to figure out the minimum number of edges among all $$$k$$$-encodings for each $$$k$$$ from $$$1$$$ to $$$q$$$.

Input:

The first line contains two integers $$$n$$$ and $$$q$$$ ($$$1 \le n \le 25\,000$$$, $$$1 \le q \le 100\,000$$$).

The second line contains $$$n$$$ integers $$$a_1, a_2, \dots, a_n$$$ which form a permutation of $$$1, 2, \dots, n$$$.

The $$$i$$$-th of the following $$$q$$$ lines contains two integers $$$l_i$$$ and $$$r_i$$$. ($$$1 \le l_i \le r_i \le n$$$).

Output:

Print $$$q$$$ lines. The $$$k$$$-th of them should contain a single integer — The minimum number of edges among all $$$k$$$-encodings.

Sample Input:

Sample Output:

2
4
3

Sample Input:

8 4
3 7 4 8 1 5 2 6
3 6
1 6
3 8
1 8

Sample Output:

Sample Input:

10 10
10 5 1 2 7 3 9 4 6 8
2 2
4 5
6 8
4 10
4 4
2 7
2 2
7 8
3 7
2 10

Sample Output:

Note:

For the first test case:

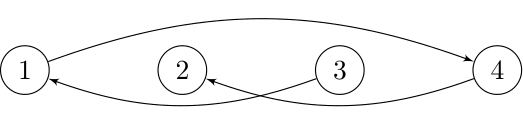
All $$$1$$$-similar permutations must allow the interval $$$[1, 3]$$$ to hold its shape. Therefore, the set of all $$$1$$$-similar permutations is $$$\{[3, 4, 2, 1], [3, 4, 1, 2], [2, 4, 1, 3], [2, 3, 1, 4]\}$$$. The optimal encoding of these permutations is $\text{[math]}$
All $$$2$$$-similar permutations must allow the intervals $$$[1, 3]$$$ and $$$[2, 4]$$$ to hold their shapes. Therefore, the set of all $$$2$$$-similar permutations is $$$\{[3, 4, 1, 2], [2, 4, 1, 3]\}$$$. The optimal encoding of these permutations is $\text{[math]}$
All $$$3$$$-similar permutations must allow the intervals $$$[1, 3]$$$, $$$[2, 4]$$$, and $$$[1, 4]$$$ to hold their shapes. Therefore, the set of all $$$3$$$-similar permutations only includes $$$[2, 4, 1, 3]$$$. The optimal encoding of this permutation is $\text{[math]}$

Informação

Provedor Codeforces

Código CF1508F