Preparando MOJI
You are given a set of $$$n$$$ segments on a line $$$[L_i; R_i]$$$. All $$$2n$$$ segment endpoints are pairwise distinct integers.
The set is laminar — any two segments are either disjoint or one of them contains the other.
Choose a non-empty subsegment $$$[l_i, r_i]$$$ with integer endpoints in each segment ($$$L_i \le l_i < r_i \le R_i$$$) in such a way that no two subsegments intersect (they are allowed to have common endpoints though) and the sum of their lengths ($$$\sum_{i=1}^n r_i - l_i$$$) is maximized.
The first line contains a single integer $$$n$$$ ($$$1 \le n \le 2 \cdot 10^3$$$) — the number of segments.
The $$$i$$$-th of the next $$$n$$$ lines contains two integers $$$L_i$$$ and $$$R_i$$$ ($$$0 \le L_i < R_i \le 10^9$$$) — the endpoints of the $$$i$$$-th segment.
All the given $$$2n$$$ segment endpoints are distinct. The set of segments is laminar.
On the first line, output the maximum possible sum of subsegment lengths.
On the $$$i$$$-th of the next $$$n$$$ lines, output two integers $$$l_i$$$ and $$$r_i$$$ ($$$L_i \le l_i < r_i \le R_i$$$), denoting the chosen subsegment of the $$$i$$$-th segment.
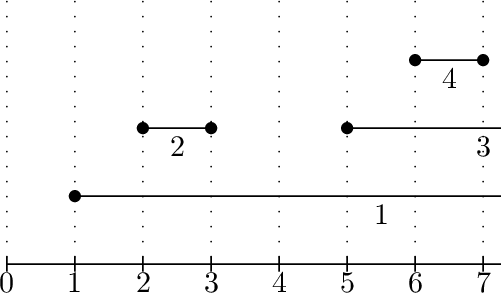
4 1 10 2 3 5 9 6 7
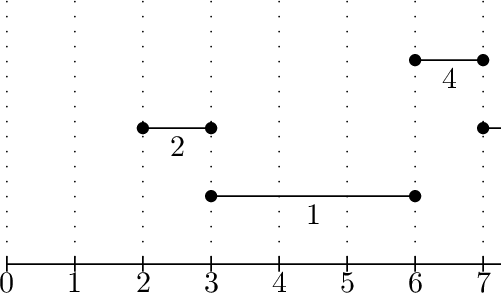
7 3 6 2 3 7 9 6 7
The example input and the example output are illustrated below. 
Informação
Provedor Codeforces
Código CF1510H
Tags
Submetido 0
BOUA! 0
Taxa de BOUA's 0%
Datas 09/05/2023 10:13:11
Relacionados